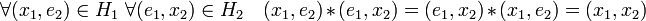Produit direct (groupes) - Définition

Introduction

En mathématiques et plus précisément dans le cadre de la théorie des groupes, le produit direct est une méthode permettant, à partir de plusieurs groupes, d'en construire un nouveau.

Le produit direct correspond à une extension dans le sens où la structure obtenue contient des sous-structures isomorphes à celles définissant le produit. Cette méthode, appliquée aux groupes permet de classifier les trois grands cas de groupes abéliens : ceux fini, ceux de type fini et les groupes de Lie de dimension finie et ayant un nombre fini de composantes connexes.

Dans tout cet article, n est un entier strictement positif, (G₁,*₁), (G₂,*₂) ... (G_n,*_n) désignent des groupes, d'éléments neutres respectifs e₁, e₂, ..., e_n.

Motivation

Le produit direct correspond à l'opération du produit cartésien avec le transfert de l'opération des groupes. Une généralisation du produit cartésien pour rendre compatible une structure algébrique est fréquente, on peut citer par exemple l'espace vectoriel, le module sur un anneau, l'algèbre sur un corps ou encore dans une moindre mesure (car l'intégrité, si elle existait, disparaît) l'anneau.

Cette approche offre un premier service : le produit direct est un outil permettant de construire de nouveaux groupes, il étend ainsi le nombre d'exemples aisément accessibles pour étudier la théorie.

Il existe un autre intérêt plus profond, celui de la classification des éléments de la structure étudiée. La classification permet de connaître, pour chaque élément les propriétés exactes dont il bénéficie ainsi que les autres éléments de la structure bénéficiant des mêmes propriétés. Un exemple de classification est celui des espaces vectoriels sur un corps K de dimension finie. La dimension classifie exactement tous ces espaces vectoriels.

Une approche fréquente est celle de l'extension, elle consiste, à partir par exemple d'un groupe, à construire un nouveau groupe contenant le précédent. En ce sens, le produit direct est une extension d'un groupe. Cette méthode, d'extension par produit, est celle utilisée pour les espaces vectoriel et tout espace vectoriel sur K de dimension finie est isomorphe à un produit de l'espace vectoriel K (de dimension un). Plus l'espace des objets construits grâce à l'extension est vaste, plus le champ d'application de l'extension est large.

Dans le cas des groupes, le produit direct est une technique d'extension couvrant très largement le cas commutatif. Si le groupe est abélien et possède suffisamment de bonnes propriétés, alors il est produit direct de groupes abéliens de la même catégorie et sa structure est particulièrement simple. Les trois cas les plus importants sont cités dans cet article.

Dans le cas non abélien, d'autres méthodes d'extension sont nécessaires, c'est la raison d'être, par exemple du produit semi-direct.

Propriétés

Propriétés élémentaires

Dans le cas où G₁ et G₂ sont de cardinaux finis, les propriétés du produit cartésien montrent que :

• L'ordre de G est égal au produit des ordres de G₁ et G₂.
• Si G₁ et G₂ sont deux groupes abéliens alors leur produit direct l'est aussi.

Cette propriété est une conséquence directe de la définition. En effet, si G₁ et G₂ sont deux groupes abéliens :

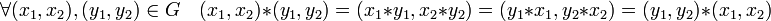
Dans le cas général, notons i₁ (resp. i₂) l'application de G₁ (resp. G₂) dans G qui à x associe (x, e₂) (resp. (e₁, x). Le sous-groupe image de i₁ (resp. i₂) est noté H₁ (resp. H₂). Enfin l'application s₁ (resp. s₂) de G dans G₁ (resp. G₂) est défini par s₁(x₁, x₂) = x₁ (resp. s₂(x₁, x₂) = x₂).

• Les applications i₁ et i₂ sont des morphismes injectifs.
• Les applications s₁ et s₂ sont des morphismes surjectifs.
• Les deux suites suivantes sont des suites exactes.

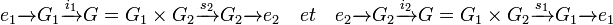
Sous-groupes H₁ et H₂

Ici, H₁ et H₂ désignent les sous-groupes G₁ x {e} et {e} x G₂. Les sous-groupes H₁ et H₂ possèdent des propriétés caractéristiques d'un produit de groupes :

• H₁ (resp. H₂) est un sous-groupe distingué isomorphe à G₁ et (resp. G₂).

En effet, H₁ est l'image de G₁ par i₁ un morphisme injectif, les deux structures sont donc isomorphes. De plus H₁ est le noyau de s₂, c'est donc un sous-groupe distingué. Un raisonnement analogue montre le résultat équivalent pour H₂.

• Tout élément de G s'écrit de manière unique comme produit d'un élément de H₁ et d'un élément de H₂.

Cette proposition est une conséquence immédiate de la définition de produit direct :

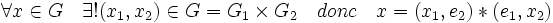
• Tout élément de H₁ commute avec tout élément de H₂.

Par définition un élément de H₁ (resp. H₂) est de la forme (x₁, e₂) (resp. (e₁, x₂)), en conséquence :