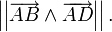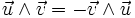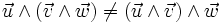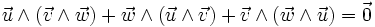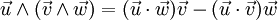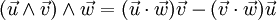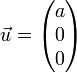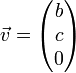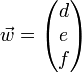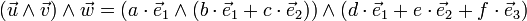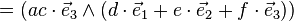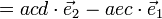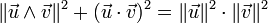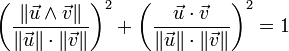Produit vectoriel - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Propriétés algébriques
Le produit vectoriel est un produit distributif, anticommutatif, non associatif :
- Distributivité sur l'addition :
,
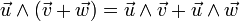
- Compatibilité avec la multiplication par un scalaire :
,
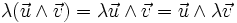
- Antisymétrie :
- Non-associativité :
Ces propriétés découlent immédiatement de la définition du produit vectoriel par le produit mixte et des propriétés algébriques du déterminant.
Comme crochet de Lie, le produit vectoriel satisfait l'identité de Jacobi :
D'autre part, il satisfait aux identités de Lagrange (Égalités du Double produit vectoriel) :
Soient 
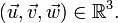
On construit une base orthonormée 
directe de 
: On pose 
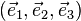
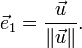
Ensuite on choisit 
comme étant l'unique vecteur directement orthogonal à 
dans le plan définit par 
.
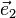
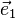
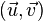
Enfin on pose 
tel que 
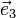
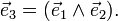
Dans cette base, les vecteurs 
ont pour coordonnées :
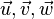
Avec 
.
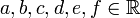
Ainsi :
De même : 
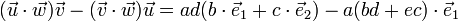
D'où l'égalité.
En partant de l'identité algébrique :
,
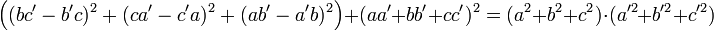
on peut démontrer facilement l'égalité (Identité de Lagrange) :
que l'on peut aussi écrire sous la forme :
ce qui équivaut à l'identité trigonométrique :
,
et qui n'est rien d'autre qu'une des façons d'écrire le théorème de Pythagore.
Invariance par isométries
Le produit vectoriel est invariant par l'action des isométries vectorielles directes. Plus exactement, pour tous vecteurs u et v de E et pour toute rotation f de E, on a :
![f\left[u\wedge v\right]=f(u)\wedge f(v)](https://static.techno-science.net/illustration/Definitions/autres/8/8fa9e4ab3d8fa937113de46509c5995b_a36e60a6a2a8f49397389cb3f6218b21.png)
.
Cette identité peut être prouvée différemment suivant l'approche adoptée :
Définition géométrique : L'identité est immédiate avec la première définition, car f préserve l'orthogonalité, l'orientation et les longueurs.
Produit mixte : L'isomorphisme linéaire f laisse invariant le produit mixte de trois vecteurs. En effet, le produit mixte de f(u), f(v), f(w) peut être calculé dans l'image par f de la base orthonormée directe dans la quelle le produit mixte de u, v et w est calculé. De fait, l'identité précédente s'obtient immédiatement :
![(f(u)\wedge f(v))\cdot f(w)=[f(u),f(v),f(w)]=[u,v,w]=(u\wedge v)\cdot w\,](https://static.techno-science.net/illustration/Definitions/autres/d/d2e011013b50c4482924d4acdb0d859e_5c3bc7016553d1551cfbf8292d69e499.png)
.
Applications
Mécanique
On définit l'opérateur rotationnel comme suit :
.
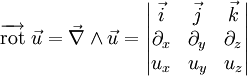
En mécanique du solide, c'est une opération très employée notamment dans la relation de Varignon qui lie les deux champs vectoriels d'un torseur. D'autre part, les équations de Maxwell sur l'électromagnétisme s'expriment à travers l'opérateur rotationnel, ainsi que les équations de la mécanique des fluides, notamment celles de Navier-Stokes.
Le moment d'une force est défini comme le produit vectoriel de cette force 
par le vecteur 
reliant son point d'application A au pivot P considéré :
.
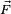
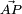
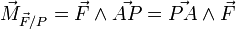
C'est une notion primordiale en mécanique du solide.
Géométrie plane
On considère ABCD un parallélogramme, c'est-à-dire qu'on a la relation
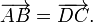
Comme indiqué plus haut dans la définition, l'aire de ce parallélogramme est égale à norme du produit vectoriel de deux vecteurs sur lesquels il s'appuie, par exemple à
