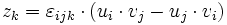Produit vectoriel - Définition
La liste des auteurs de cet article est disponible ici.
Notation
Plusieurs notations sont en concurrence pour le produit vectoriel :
- En France, le produit vectoriel de u et de v est noté
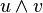
- Dans la littérature anglophone (et au Canada francophone, ainsi qu'en Suisse), le produit vectoriel est noté
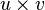
- Une troisième notation est l'utilisation des crochets de Lie :
![\left[\vec u\, , \vec v\right]](https://static.techno-science.net/illustration/Definitions/autres/b/b64097a603bfcb40c1a761a107e2e945_52c1400a7e8d3204b18b149de5747cf2.png)
Dans cet article, nous utiliserons la première convention.
Définitions alternatives
Comme produit de Lie
Toute isométrie directe de R3 est une rotation vectorielle. L'ensemble des isométries directes forme un groupe de Lie classique noté SO(3) (autrement dit, un sous-groupe fermé de GL3(R)). Son algèbre de Lie, notée so(3) est la sous-algèbre de Lie de gl3(R) définie comme l'espace tangent de SO(3) en l'identité. Un calcul direct montre qu'il est l'espace des matrices antisymétriques de taille 3. Cet espace est a fortiori stable par le crochet de Lie.
Toute matrice antisymétrique M de taille 3 s'écrit de manière unique :
-
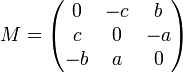
En identifiant M et le vecteur (a, b, c), on définit un isomorphisme linéaire entre so(3) et R3. Le crochet de Lie se transporte via cet isomorphisme, et R3 hérite d'une structure d'algèbre de Lie. Le crochet [u, v] de deux vecteurs est précisément le produit vectoriel de u et de v.
En effet, si u1=(a1, b1, c1), et u2=(a2, b2, c2), leur crochet se calcule en introduisant les matrices antisymétriques correspondantes M1 et M2 :
Le vecteur correspondant, à savoir [u1,u2], a donc pour coordonnées (b1c2-b2c1, a2c1-a1c2, a1b2-a2b1). Cette approche redéfinit donc le produit vectoriel.
Si on suit cette approche, il est possible de prouver directement l'invariance du produit vectoriel par isométries
-
![f\left[u\wedge v\right]=f(u)\wedge f(v)](https://static.techno-science.net/illustration/Definitions/autres/8/8fa9e4ab3d8fa937113de46509c5995b_a36e60a6a2a8f49397389cb3f6218b21.png)
En tant qu'algèbres de Lie, so(3) a été identifié à R3. L'action (linéaire) de SO3(R) sur R3 s'identifie à l'action par conjugaison sur so(3). SO3(R) opère donc par automorphisme d'algèbres de Lie. Autrement dit, l'identité ci-dessus est vérifiée.
Comme produit de quaternions imaginaires
Il est possible de retrouver produit vectoriel et produit scalaire à partir du produit de deux quaternions purs. Pour rappel, le corps (non commutatif) des quaternions H est l'unique extension de R de dimension 4. Sa base canonique est (1,i, j, k) où le sous-espace engendré par i, j, k forme l'espace des quaternions purs, canoniquement identifié avec R3. Ces éléments vérifient :
-
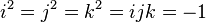
-
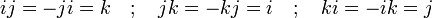
Si q1=a1i+b1j+c1k et q2 = a2i+b2j+c2k, le produit q1q2 se calcule immédiatement :
- q1q2 = − (a1a2 + b1b2 + c1c2) + (b1c2 − b2c1)i + (c1a2 − c2a1)j + (a1b2 − a2b1)k.
La partie réelle est au signe près le produit scalaire de q1 et de q2, la partie imaginaire est un quaternion pur qui correspond au produit vectoriel, après identification avec R3.
Cette coïncidence trouve ses explications dans le paramétrage du groupe SO(3) par les quaternions unitaires.
L'application linéaire envoyant 1 sur 1, i sur -i, j sur -j et k sur -k est appelée la conjugaison. Le conjugué d'un quaternion q est noté
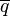
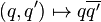
-
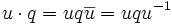
Cette action préserve la norme ; autrement dit, c'est une action par isométries. Elle définit donc un morphisme de groupes :
Ce morphisme est en réalité le revêtement universel du groupe SO(3). Il induit donc un isomorphisme entre les algèbres de Lie.
L'algèbre de Lie de S3 est justement l'espace des quaternions imaginaires munis du crochet de Lie obtenu comme la partie imaginaire du produit des quaternions. Cette algèbre de Lie est isomorphe à l'algèbre de Lie R3 (muni du produit vectoriel).
C'est la raison fondamentale pour laquelle la partie imaginaire de deux quaternions imaginaires s'identifie au produit vectoriel.
Il est de nouveau possible de justifier l'invariance par isométrie. Toute isométrie de l'espace des quaternions imaginaires s'écrit comme la conjugaison par un quaternion unitaire. Si q est un quaternion unitaire, et q1, q2 sont des quaternions imaginaires, il suffit de constater :
pour en déduire l'invariance par isométrie du produit vectoriel.
Par le produit tensoriel
Soient deux vecteurs à trois composantes ui et vj. On peut définir le tenseur
qui, en notation tensorielle, s'écrit simplement :
Ce tenseur peut se décomposer en la demi-somme de deux tenseurs, l'un complètement symétrique :
qui a 6 composantes indépendantes, et l'autre complètement anti-symétrique :
qui a 3 composantes indépendantes. On peut alors « transformer » ce tenseur anti-symétrique en un vecteur à trois composantes en utilisant le symbole de Levi-Civita
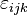
(selon la convention de sommation d'Einstein, on somme sur i et sur j dans la formule ci-dessus). Le vecteur zk est le produit vectoriel de ui et vj.
On voit que si l'on échange les indices i et j, le signe change, ce qui illustre l'antisymétrie du produit vectoriel. En outre le résultat est un « pseudovecteur » puisqu'il est renversé si on change l'orientation de l'espace.
![[M_1,M_2]=M_1M_2-M_2M_1=\begin{pmatrix} 0 & a_2b_1-a_1b_2 & a_2c_1-a_1c_2\\ a_1b_2 -a_2b_1 & 0 & b_2c_1-b_1c_2\\ a_1c_2-a_2c_1 & b_1c_2-b_2c_1 & 0 \end{pmatrix}](https://static.techno-science.net/illustration/Definitions/autres/4/40b2b006a746b2f462fc807be7b8ace9_a4a1f5f79a0ff11f3404d5cd727daa9e.png)
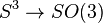
![\left[qq_1\overline{q}\right].\left[qq_2\overline{q}\right]=q(q_1q_2)\overline{q}](https://static.techno-science.net/illustration/Definitions/autres/0/02defb56e8ee81404bea862ef03b3d18_07c3b1780e5363ae744837b74112e634.png)
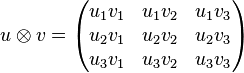
![[u\otimes v]_{ij}= u_i\cdot v_j](https://static.techno-science.net/illustration/Definitions/autres/d/d261f6239a5c3ddfd2ba282e6dd92a49_95c6601cab524b9bcc8ceb582dac77c6.png)
![[u\odot v]_{ij}=u_i\cdot v_j + u_j\cdot v_i](https://static.techno-science.net/illustration/Definitions/autres/5/5ab63f5fe1cc8c4a8a4893182d42881e_ae806d699dabf304dca82827b0114b93.png)
![[u\wedge v]_{ij}=u_i\cdot v_j - u_j\cdot v_i](https://static.techno-science.net/illustration/Definitions/autres/4/4723e4a41e870debba5d01dd5b6ded82_db22faf8152f75358382e600165f2543.png)