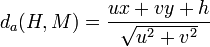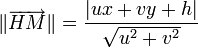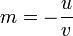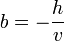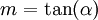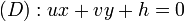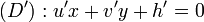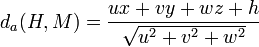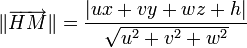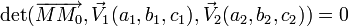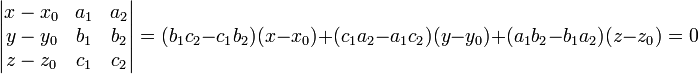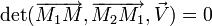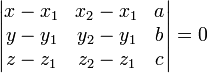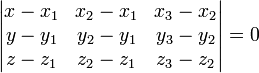Propriétés métriques des droites et plans - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie euclidienne, c'est-à-dire dans le plan et l'espace muni d'une distance et d'un produit scalaire, les droites et les plans possèdent des propriétés métriques permettant de les caractériser grâce à un point et un vecteur, dit normal. On peut aussi calculer la distance qui les sépare d'un point donné ou bien calculer celle qui sépare deux droites ou deux plans. On peut aussi calculer l'angle formé par deux droites ou deux plans.
Dans cet article, on a muni le plan ou l'espace d'un repère orthonormal dans lequel sont exprimées toutes les coordonnées. Toute droite du plan y possède une équation du type ux + vy + h = 0 où (u , v) est différent de (0 , 0) et tout plan de l'espace possède une équation de la forme ux + vy + wz + h = 0 où (u, v, w) est différent de (0, 0, 0)
La droite dans le plan euclidien
Vecteur normal à une droite
Soit M(x,y) un point de la droite D dont une équation dans un repère orthonormal est donnée par :
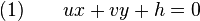
et M0(x0,y0) un point spécifique de D, On a :
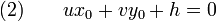
En retranchant (2) à (1) on obtient :
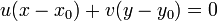
En notant
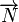
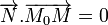
La droite d'équation ux + vy + h = 0 est donc orthogonale au vecteur
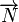
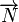
Droite passant par un point et orthogonale à un vecteur non nul donné
Soit un point M(x,y) et un vecteur
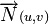
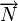
La droite D, passant par M0(x0,y0) et orthogonale à
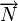
Distance algébrique d'un point M(x,y) à une droite d'équation ux + vy + h = 0
Soit H la projecté de M(x,y) sur D avec
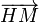
La droite perpendiculaire à D et passant par M étant orientée suivant la direction du vecteur
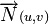
En valeur absolue:
Droite et pente
Pour v non nul, la droite D d'équation ux + vy + h = 0 possède une équation sous la forme mx + b = y avec
et
La pente d'une droite est le réel
L'angle α représente l'angle entre l'axe des abscisses et la droite D.
Équation normale d'une droite
Dans le repère

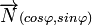

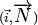
L'équation (1) s'écrit :
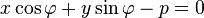
Angles de deux droites
Soit D et D' deux droites d'équations
L'angle formé par les deux droites est connu par sa tangente:
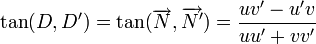
Le plan dans l'espace euclidien
Vecteur orthogonal à un plan
Soit M(x,y,z) un point du plan P dont l'équation dans un repère orthonormé est donnée par :
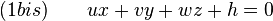
Pour M0(x0,y0,z0) un point spécifique de P on obtient :
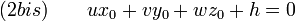
En retranchant (2bis) à (1bis) on obtient :
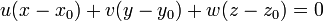
En notant
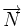
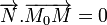
Le plan P d'équation ux + vy + wz + h = 0 est donc orthogonal au vecteur
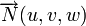
Plan passant par un point et orthogonal à un vecteur non nul donné
Soit un point
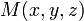
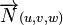
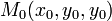
Le plan P, passant par M0(x0,y0,z0) et orthogonal à
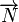
Distance algébrique d'un point M(x,y,z) à un plan P d'équation ux + vy + wz + h = 0
Soit H la projeté de M(x,y,z) sur P avec
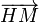
La droite perpendiculaire à P et passant par M étant orientée suivant la direction du vecteur
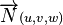
En valeur absolue:
Angles de deux plans
Soitent (P) et (P') deux plans d'équations
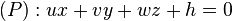
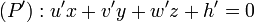
L'angle géométrique (P,P') est déterminé à l'aide de l'angle des vecteurs normaux
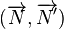
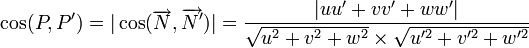
Plans perpendiculaires
Les plan (P) et (P') sont perpendiculaires si les vecteurs normaux
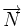
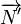
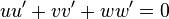
Équation de plan et déterminant
Plan défini par un point et deux vecteurs non colinéaires
Soient un point M0(x0,y0,z0) et deux vecteurs
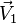
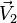
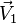
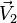
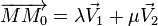
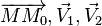
Ce qui donne, en représentant le produit mixte de ces trois vecteurs sous la forme d'un déterminant :
Son équation est :
que l'on peut écrire sous la forme ux + vy + wz + h = 0
Plan défini par deux points et un vecteur
Soient deux points M1(x1,y1,z1),M2(x2,y2,z2) et un vecteur
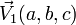
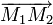
Le point M appartient au plan passant par M1(x1,y1,z1),M2(x2,y2,z2) et de direction
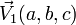
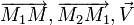
Son équation est :
Plan défini par trois points non alignés
Soient M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3), trois points non alignés.
Par analogie avec ce qui précède, l'équation du plan passant par ces trois points est