RANSAC - Définition

Introduction

RANSAC est une abréviation pour "RANdom SAmple Consensus". Il s'agit d'une méthode itérative pour estimer les paramètres d'un modèle mathématique à partir d'un ensemble de données observées qui contient des valeurs aberrantes ("outliers"). Il s'agit d'un algorithme non-déterministe dans le sens où elle produit un résultat correct seulement avec une certaine probabilité, cette probabilité augmentant à mesure que le nombre d'itérations est grand. L'algorithme a été publié pour la première fois par Fischler et Bolles en 1981.

L’hypothèse de base est que les données sont constituées de "inliers", à savoir les données dont la distribution peut être expliquée par un ensemble de paramètres d'un modèle, et de "outliers" qui sont des données qui ne correspondent pas au modèle choisi. De plus, les données peuvent être soumises au bruit. Les valeurs aberrantes (outliers) peuvent venir, par exemple, des valeurs extrêmes du bruit, de mesures erronées ou d'hypothèses fausses quant à l'interprétation des données. RANSAC suppose également que, étant donné un ensemble (généralement petit) d’inliers, il existe une procédure qui permet d'estimer les paramètres d'un modèle de telle façon à expliquer de manière optimale ces données.

Exemple

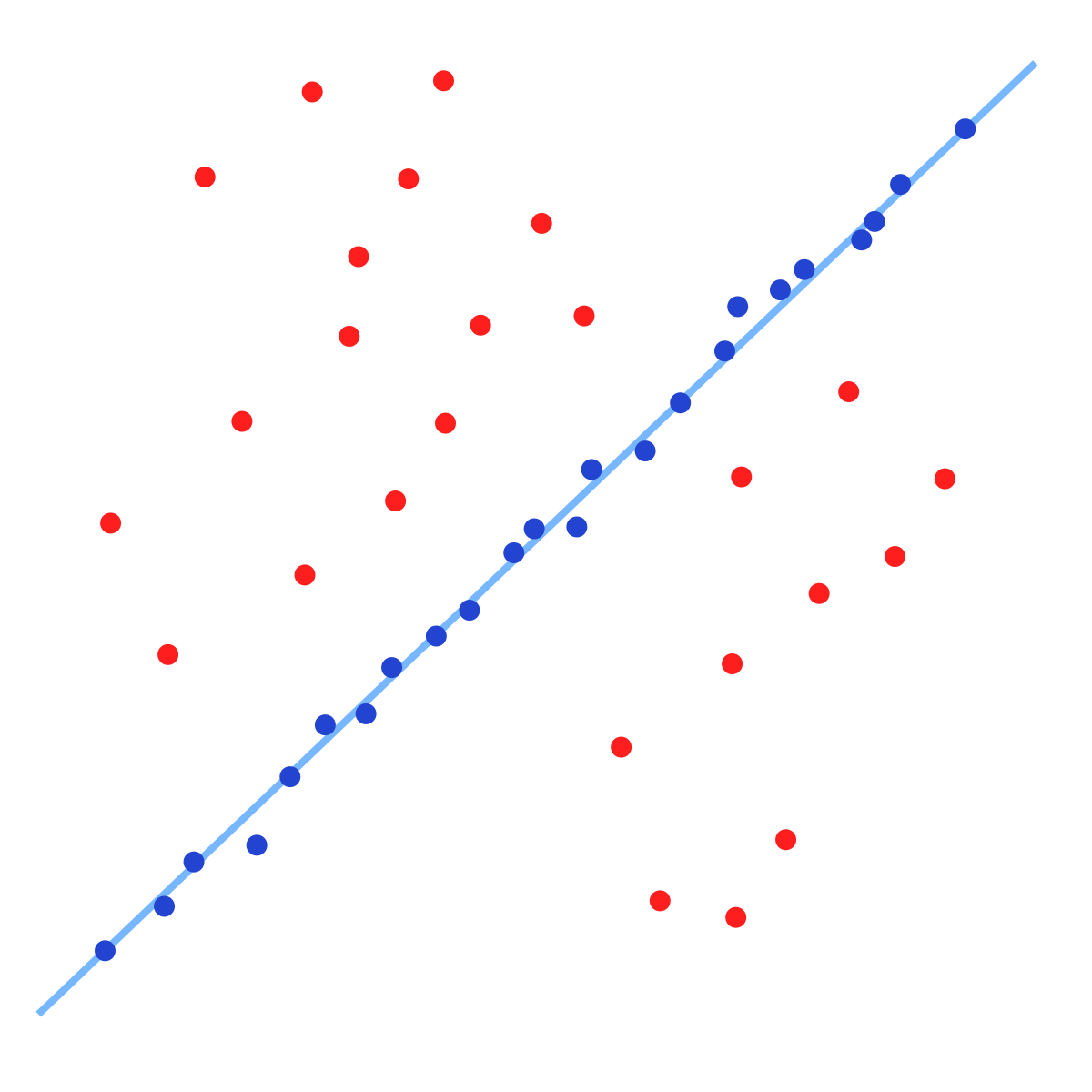
Un exemple simple est l'ajustement d'une ligne 2D à une série d'observations. On suppose que cet ensemble contient à la fois des inliers, c'est-à-dire, les points qui peuvent être approximativement ajustés à une ligne, et les outliers (valeurs aberrantes), les points qui sont éloignés de ce modèle de ligne. Un simple traitement par une méthode des moindres carrés donnera une ligne qui est mal ajustée aux inliers. En effet, la droite s'ajustera de manière optimale à tous les points, y compris les valeurs aberrantes (outliers). RANSAC, par contre, peut générer un modèle qui ne tiendra compte que des inliers, à condition que la probabilité de choisir seulement que des inliers dans le choix des données soit suffisamment élevée. Cependant, il n'y a aucune garantie d'obtenir cette situation, et il existe un certain nombre de paramètres de l'algorithme qui doivent être soigneusement choisis pour maintenir ce niveau de probabilité suffisamment élevée.

Un jeu de données avec de nombreuses valeurs aberrantes pour lequel une ligne doit être ajustée.

Ligne ajustée avec la méthode RANSAC, les valeurs aberrantes n'ont aucune influence sur le résultat.

L'algorithme

L'algorithme RANSAC générique, en pseudocode, fonctionne comme suit:

      entrées:          data - un ensemble d'observations          modele - un modèle qui peut être ajusté à des données          n - le nombre minimum de données nécessaires pour ajuster le modèle          k - le nombre maximal d'itérations de l'algorithme          t - une valeur seuil pour déterminer si une donnée correspond à un modèle          d - le nombre de données proches des valeurs nécessaires pour faire valoir que le modèle correspond bien aux données      

      sorties:          meilleur_modèle - les paramètres du modèle qui correspondent le mieux aux données (ou zéro si aucun bon modèle a été trouvé)          meilleur_ensemble_points - données à partir desquelles ce modèle a été estimé          meilleure_erreur - l'erreur de ce modèle par rapport aux données            itérateur:= 0      meilleur_modèle:= aucun      meilleur_ensemble_points:= aucun      meilleure_erreur:= infini      tant que itérateur < k          points_aléatoires:= n valeurs choisies au hasard à partir des données          modèle_possible:= paramètres du modèle correspondant aux points_aléatoires          ensemble_points:= points_aléatoires                Pour chaque point des données pas dans points_aléatoires              si le point s'ajuste au modèle_possible avec une erreur inférieure à t                  Ajouter un point à ensemble_points                    si le nombre d'éléments dans ensemble_points est > d              (ce qui implique que nous avons peut-être trouvé un bon modèle,              on teste maintenant dans quelle mesure il est correct)              modèle_possible:= paramètres du modèle réajusté à tous les points de ensemble_points              erreur:= une mesure de la manière dont ces points correspondent au modèle_possible              si erreur < meilleure_erreur                  (nous avons trouvé un modèle qui est mieux que tous les précédents,                  le garder jusqu'à ce qu'un meilleur soit trouvé)                  meilleur_modèle:= modèle_possible                  meilleur_ensemble_points:= ensemble_points                  meilleure_erreur:= erreur                     incrémention de l’itérateur            retourne meilleur_modèle, meilleur_ensemble_points, meilleure_erreur      

Variantes possibles de l'algorithme RANSAC :

• Arrêter la boucle principale si un modèle assez bon a été trouvée, c'est-à-dire avec une erreur suffisamment petite. Peut sauver du temps de calcul, au détriment d'un paramètre supplémentaire.
• Calculer erreur directement à partir de modèle_possible, sans ré-estimation du modèle à partir de ensemble_points. Peut faire gagner du temps au détriment de la comparaison des erreurs liées à des modèles qui sont estimés à partir d'un petit nombre de points et donc plus sensibles au bruit.