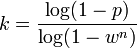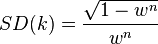RANSAC - Définition

Présentation

Les données d'entrée de l'algorithme RANSAC sont un ensemble de valeurs des données observées, un modèle paramétré qui peut expliquer ou être ajusté aux observations, et des paramètres d'intervalle de confiance.

RANSAC atteint son objectif en sélectionnant itérativement un sous-ensemble aléatoire des données d'origine. Ces données sont d'hypothétiques inliers et cette hypothèse est ensuite testé comme suit:

1. Un modèle est ajusté aux inliers hypothétiques, c'est-à-dire que tous les paramètres libres du modèle sont estimés à partir de cet ensemble de données.
2. Toutes les autres données sont ensuite testées sur le modèle précédemment estimé. Si un point correspond bien au modèle estimé alors il est considéré comme un inlier candidat.
3. Le modèle estimé est considéré comme correct si suffisamment de points ont été classés comme inliers candidats.
4. Le modèle est re-estimé à partir de cet ensemble des inliers candidats.
5. Finalement, le modèle est évalué par une estimation de l'erreur des inliers par rapport au modèle.

Cette procédure est répétée un nombre fixe de fois, chaque fois produisant soit un modèle qui est rejeté parce que trop peu de points sont classés comme inliers, soit un modèle réajusté et une mesure d'erreur correspondante. Dans ce dernier cas, on conserve le modèle réévalué si son erreur est plus faible que le modèle précédent.

Avantages et inconvénients

Un avantage de RANSAC est sa capacité à faire des statistiques robustes des paramètres du modèle, c'est-à-dire, qu'il peut estimer les paramètres avec un degré élevé de précision, même si une quantité importante de valeurs aberrantes (outliers) est présente dans l'ensemble de données. Un inconvénient de RANSAC est qu'il n'y a pas de limite supérieure sur le temps qu'il faut pour calculer ces paramètres. Quand un temps limite supérieure est utilisé (un nombre maximal d'itérations), la solution obtenue peut ne pas être la solution optimale. Un autre inconvénient de RANSAC est qu'elle suppose de fixer des seuils spécifiques au problème traité.

RANSAC ne peut estimer qu'un seul modèle à un ensemble de données particulier. Comme pour tout approche à modèle unique, lorsque deux (ou plusieurs) modèles coexistent, RANSAC peut ne parvenir à trouver ni l'un ni l'autre.

Les paramètres

Les valeurs des paramètres t et d doivent être fixées conformément aux exigences spécifiques liées à l'application et à l'ensemble de données. qui peuvent être éventuellement fondées sur l'évaluation expérimentale. Le paramètre k (le nombre d'itérations), cependant, peut être déterminée à partir d'un résultat théorique. Soit p la probabilité que l'algorithme RANSAC pendant une itération sélectionne uniquement des inliers dans l'ensemble des données d'entrée, lorsqu'il choisit les n points à partir desquels les paramètres du modèle seront estimés. Lorsque cela se produit, le modèle qui en résulte est susceptible d'être pertinent, donc p donne la probabilité que l'algorithme produise un résultat correct. Soit w, la probabilité de choisir un inlier à chaque fois qu'un seul point est sélectionné, c'est-à-dire

w = nombre de inliers dans les données / nombre de points dans les données

Un cas habituel est que w ne soit pas connu à l'avance, mais une valeur approximative peut être estimée. En supposant que les n points nécessaires pour l'estimation d'un modèle sont sélectionnées de manière indépendante, wⁿ est la probabilité que l'ensemble des n points correspond à des inliers et 1 − wⁿ est la probabilité qu'au moins un des n points est un cas atypique (outlier), un cas qui implique qu'un mauvais modèle sera estimé à partir de cet ensemble de points. Cette probabilité à la puissance de k est la probabilité que l'algorithme ne choisissent jamais un ensemble de n points qui seraient tous des inliers et cela doit être égale à 1 − p. Par conséquent,

1 − p = (1 − wⁿ)^k

qui, en prenant le logarithme des deux côtés, conduit à

Il convient de noter que ce résultat suppose que les n points de données sont sélectionnés de façon indépendante, c'est-à-dire, qu'un point qui a été sélectionné une fois est remis et peut être sélectionné à nouveau dans la même itération. Cela n'est pas souvent une approche pertinente et la valeur calculée pour k devrait être pris comme une limite supérieure dans le cas où les points sont choisis sans remise. Par exemple, dans le cas de la recherche d'une ligne qui s'ajuste à la série de données illustrée sur la figure ci-dessus, l'algorithme RANSAC choisit généralement deux points à chaque itération et calcule le modèle_possible comme la ligne qui relie ces deux points et il est alors important que les deux points soient distincts.

Pour gagner en qualité, l'écart type ou des multiples de celui-ci peuvent être ajouté à k. L'écart type de k est définie comme