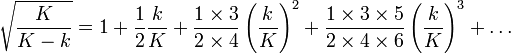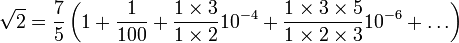Racine carrée de deux - Définition

Méthodes numériques d'approximation

√2 vaut approximativement 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 990 732 478 462 107 038 850 387 534 327 641 572 7

Ces décimales constituent la suite A002193 de l’OEIS.

Le calcul d’une valeur approchante de √2 a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d’extraction de racines carrées. En informatique, ces recherches se sont poursuivies afin d’optimiser ces algorithmes en réduisant les temps de calcul et la consommation de mémoire.

Les méthodes numériques d’approximation présentées ci-dessous sont destinées au calcul d’un nombre important de décimales. Elles se basent généralement sur une suite convergente de nombres rationnels ; ainsi l’itération s’affranchit du coût de calcul sur des nombres à virgule flottante — dont il faudrait en plus connaître la précision a priori. Les meilleures approximations par une suite rationnelle p_n/q_n donnent une erreur en 1/q_n², une propriété de l’approximation diophantienne des entiers quadratiques.

Méthodes à convergence linéaire

Méthode de Théon de Smyrne

On doit à Théon de Smyrne ces deux suites (p_n) et (q_n) définies par récurrence :

p_{n + 1} = p_n + 2q_n,     p₀ = 1 ;

q_{n + 1} = p_n + q_n,     q₀ = 1.

Ces suites sont à valeur entière strictement positive, donc strictement croissantes par récurrence, et vérifient

p_n² − 2q_n² = (−1)ⁿ(p₀² − 2q₀²)

de sorte que p_n/q_n tend vers √2.

On ne sait pas si l’intention de Théon de Smyrne était de calculer une valeur approchée de √2.

Solutions de l'équation diophantienne a²− 2b² = k

Les solutions entières de l’équation a² − 2b² = k sont générées par récurrence

a_{m + 1} = 3a_m + 4b_m

b_{m + 1} = 2a_m + 3b_m

à partir des valeurs initiales (a₀, b₀) = (1, 1) pour k = −1 et (3, 2) pour k = 1.

Cette méthode est déduite de celle de Théon : chaque itération de la présente correspond à deux itérations de celle-là. Ainsi, a_n/b_n tend linéairement vers √2.

Les premières solutions sont :

• k = −1 :  (1, 1),  (7, 5),  (41, 29),  (239, 169),  (1393,985),
• k =   1 :  (3, 2),  (17, 12),  (99, 70),  (577, 408),  (3363, 2378).

Les deux approximations mises en gras furent utilisées en pratique par les arpenteurs anciens :

• 28 : 20  avec l’erreur relative de – 1,0051 %, brièvement au début du III^e millénaire av. J.-C. par les Égyptiens Anciens (cf. le remen de construction) et
• 99 : 70  avec l’erreur relative de + 0,0051 %, tout au long de l’histoire et dans beaucoup de pays dans la triangulation rationnelle du carré selon les arpenteurs.

Méthode de Théon généralisée

On se donne (a, b), obtenues par la méthode de Théon, qui sont donc solutions de l’une des deux équations diophantiennes précédente 2b² = a² - k = K, avec k = ±1 et K> 1. On peut alors écrire

√2 = a/b √[K/(K + k)]

Les suites p_n et q_n définies par

p_{n + 1} = (2K + k)p_n + 2Kq_n,     p₀ = 1 ;

q_{n + 1} = (2K + 2k)p_n + (2K + k)q_n,     q₀ = 1.

vérifient

(K + k)p_{n + 1}² - K q_{n + 1}² = (K + k)p_n² - K q_n² = … = k,

et donc, de la même façon que ci-dessus, la suite p_n/q_n converge vers √[K/(K + k)]. De plus, si k = 1, cette suite est croissante donc approche cette valeur par défaut, et si k = -1, elle est décroissante donc approche cette valeur par excès.

On peut utiliser cette relation pour estimer l’erreur :

ε_{n + 1} ≈ ε_n (4K + 3k)⁻²

et c’est une majoration si k= 1. La convergence est donc linéaire : elle fait gagner un nombre à peu près constant de décimales à chaque itération.

Cette méthode correspond à une généralisation de la méthode du paragraphe précédent au radical √[K/(K + k)]. Pour K plus grand, la suite q_n croit plus rapidement, donc la convergence est accélérée.

Premières approximations de √2 = 17/12 √(288/289) par approximation linéaire de √(288/289). Les paramètres sont a = 17, b = 12, K = 288, k = 1. On a
ε_{n + 1} < 7,5 × 10^-7ε_n   (avant approximation décimale des quotients).

itération	valeur fractionnaire	décimales exactes
0	1	1
1	19601/13860	1,41421356
2	22619537/15994428	1,41421356237309
3	26102926097/18457556052	1,41421356237309504880
4	30122754096401/21300003689580	1,41421356237309504880168872

Développement en fraction continue

Une autre méthode consiste à approcher a√2 − b par sa fraction continue généralisée pour (a, b) solutions de l’équation diophantienne 2a² = b² + k, avec k = ± 1 :

a√2 − b = [0; k, 2b; k, 2b; k, 2k, …].

m√2 − n est approximé à l’aide de la suite (p_n/q_n) déterminée par la relation de récurrence

p_{n + 1} = q_n

q_{n + 1} = 2bq_n + kp_n

L’erreur vérifie asymptotiquement

ε_{n + 1} < |a√2 − b|/(2b − 1) ε_n

Premières approximations de √2 par approximation linéaire de 169√2 − 239. Les paramètres sont a = 169, b = 239, k = 1, ε_{n + 1} ~ 4 × 10⁻⁶ ε_n.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	114243/80782	1,414213562
2	54608393/38613965	1,41421356237309
3	26102926097/18457556052	1,41421356237309504880
4	12477253282759/8822750406821	1,4142135623730950488016887

Développement en série entière

On se donne (a, b) solutions de l’équation diophantienne 2a² = b² + k = K, avec k = ±1. On peut alors écrire √[K/(K − k)] comme somme d'une série via le développement en série entière de (1+z)^½ (ou la formule du binôme généralisée, simple variante d'exposition).

et utiliser √2 = b/a √[K/(K − k)]

Dans le cas √2 = 7/5 √(50/49), ce développement se simplifie de façon remarquable comme l’a fait remarquer Leonhard Euler en 1755 :

Approximation √2 = 239/169 √(57122/57121) par le développement en série entière du radical fractionnaire. Les paramètres sont a = 239, b = 169, K = 57122, k = 1.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	239/169	1,4142
2	6238763163557/4411471739168	1.41421356237309
3	712741258857407103/503984177369508992	1.414213562373095048
4	325705649507622468308893/230308673437608741128192	1.414213562373095048801688

Dichotomie

Il est possible d’approcher √2 par bissection. Cette méthode est de convergence linéaire lente : on gagne trois décimales à chaque dizaine d’itérations.

Méthode à convergence quadratique

La méthode de Newton appliquée à la fonction racine carrée permet de calculer une valeur approchée de √2 de manière itérative avec une convergence quadratique, c’est-à-dire doublant le nombre de décimales à chaque itération. La récurrence a la forme

u_{n + 1} = u_n/2 + 1/u_n

Cet algorithme s’appelle méthode de Héron ou méthode babylonienne car il semble que ce soit celle utilisée par les babyloniens pour trouver des valeurs approchées de racines carrées.

Si l’on s’intéresse aux fractions successives à partir d’une valeur initiale p₀ et q₀, la récurrence sur le numérateur et le dénominateur sont

p_{n + 1} = p_n² + 2q_n²

q_{n + 1} = 2p_nq_n

Premières approximations de √2 données par la méthode de Newton.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	3/2	1
2	17/12	1,41
3	577/408	1,41421
4	665857/470832	1,41421356237
5	886731088897/627013566048	1,41421356237309504880168

Méthodes cubiques

Méthode de Halley

Un exemple de méthode cubique s’obtient par l’itération de Halley. Elle cherche le zéro de f(x) = x² − 2 en utilisant les deux premières dérivées. La solution itérative est

x_{n + 1} = x_n × (x_n² + 6)/(3x_n² + 2)

soit en posant x_n = p_n/q_n :

p_{n + 1} = p_n(p_n² + 6q_n²)

q_{n + 1} = q_n(3p_n² + 2q_n²)

Cette méthode est de convergence cubique : le nombre de décimales exactes triple à chaque itération.

Premières approximations de √2 données par la méthode cubique.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	7/5	1,4
2	1393/985	1,414213
3	10812186007/7645370045	1,414213562373095048
4	—	1,4142135623730950488 016887242096980785696 718753769480731766797

Méthode de Householder

L’itération de Householder appliquée à f(x) = 1/x² − 1/√2 donne une suite convergeant vers 1/√2 :

x_{n + 1} = x_n + x_n/8 × (2x_n² − 1)(6x_n² − 7)

Méthodes d'ordre supérieur

On utilise une méthode de Newton modifiée pour trouver le zéro de f(x) = 1/x² − 1/2. Cela donne la suite récurrente :

x_{n + 1} = x_n + x_n/16 × (8h_n + 6h_n² + 5h_n³)

avec

h_n = 1 − x_n²/2

Cette méthode est de convergence quartique, c’est-à-dire d’ordre 4 : le nombre de décimales exactes quadruple à chaque itération.

Premières approximations de √2 données par la méthode quartique.

itération	valeur fractionnaire	décimales exactes
0	3/2	1
1	23169/214	1,414
2	57367317478181003155381859082363/2105	1,41421356237309
3	—	1,41421356237309 5048801688724209 6980785696718753 76948073176679737

Il existe des méthodes d’ordre supérieur, notamment parmi les méthodes de Householder.