Racine carrée de deux - Définition

Introduction

La racine carrée de deux, notée √2, √2 ou 2^1/2, est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui-même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10^-9 près est 1,414213562

L’hypoténuse d’un triangle rectangle isocèle de côté 1 vaut √2.

Le calcul d’une valeur approchée de √2 a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d’extraction de racines carrées. En informatique, ces recherches se sont poursuivies afin d’optimiser ces algorithmes en réduisant les temps de calcul et la consommation de mémoire.

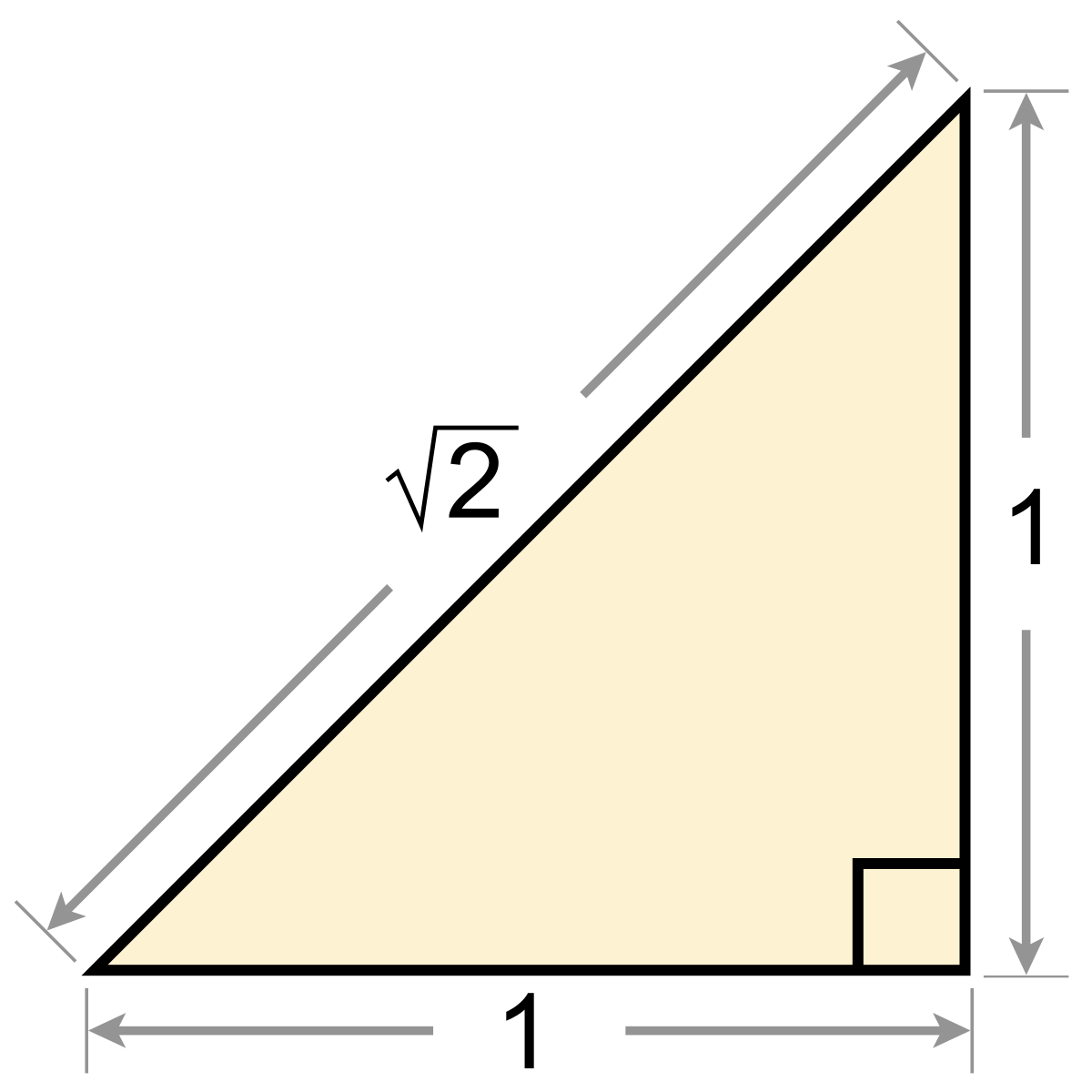
La longueur √2 peut être construite géométriquement de plusieurs manières ; par exemple, la diagonale d'un carré de côté 1, qui est l’hypoténuse d’un triangle rectangle isocèle, vaut √2 par le théorème de Pythagore.

Le nombre √2 est étudié depuis longtemps par les Babyloniens, experts en questions du second degré et disposant d'un algorithme d'approximation précis. Depuis l'école de Pythagore, les Grecs du V^e siècle av. J.-C. et du IV^e siècle av. J.-C. l'étudient pour mieux comprendre l'incommensurabilité, concept équivalent à notre irrationnalité. Ils trouvent trois démonstrations différentes, conduisant à divers progrès, comme la mise au point du raisonnement par l'absurde, la descente infinie ou encore l'anthyphérèse, un algorithme comparable à notre fraction continue. Pour les Grecs, ni les fractions, ni les irrationnels ne sont des nombres. Ce pas est franchi par les mathématiciens arabes à l'origine de l'algèbre.

Ce nombre intervient dans des applications de la vie courante :

• les feuilles de papier au format international (ISO 216) ont une proportion longueur/largeur égale à √2 ;
• en musique, le rapport des fréquences de la quarte augmentée de la gamme tempérée vaut √2 ;
• en électricité, la tension maximale du courant alternatif domestique vaut √2 de la tension efficace indiquée (généralement 110 ou 230 V) ;
• en photographie, la suite des valeurs d’ouverture du diaphragme sont les valeurs approchées d’une suite géométrique de raison √2.

Étymologie

L’expression « racine carrée » est issue de la notation géométrique européenne qui prévalait avant la notation algébrique, et plus particulièrement de l’une des constructions de √2 qui sera présentée à la  ; en effet, les problèmes mathématiques ont souvent été présentés sous forme géométrique avant d’être ramenés à des expressions algébriques. L’expression « radical de deux » était aussi utilisée.

Histoire

Babylone

Schéma de la tablette YBC 7289.

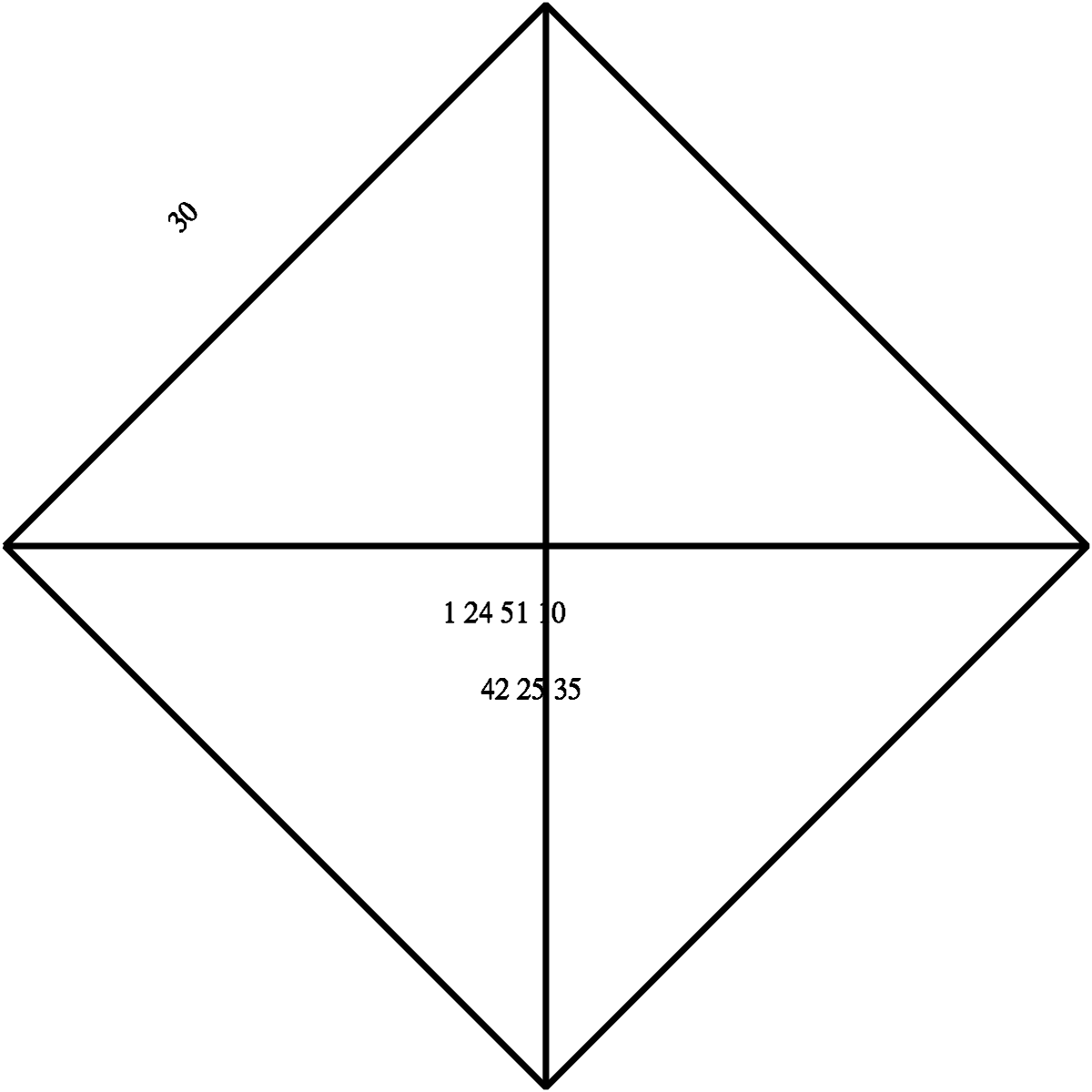
La culture mathématique babylonienne est avant tout algorithmique. Elle dispose d'un système de numération ancien et positionnelle. Certaines tablettes, comme celle notée BM 13901, montre une bonne connaissance des questions du second degré, probablement traitées à partir de méthodes géométriques. En plus de disposer de méthodes de résolution, les Babyloniens savent calculer des approximations de racines carrées. La tablette YBC 7289 donne l'approximation de √2 sous la forme suivante :

      

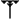
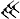
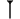
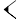
Cette écriture correspond à la meilleure approximation possible de √2 avec quatre chiffres significatifs en numération babylonienne (base 60). L'approximation est précise au millionième. Cette tablette montre plusieurs éléments remarquables, leur préoccupation mathématique n'est pas uniquement pragmatique, une telle précision est trop importante pour une application pratique. Elle dénote aussi de la connaissance d'un algorithme d'approximation de racine, probablement de type méthode de Héron et équivalent à notre fraction continue.

Grèce antique

A la fin du VI^e siècle av. J.-C., l'école pythagoricienne prend connaissance du savoir babylonien, qui s'ajoute à la tradition grecque naissante, issue de Ionie. L'orientation ionienne, dont le maître à penser est Thalès, est géométrique. La notion de démonstration entre déjà dans leurs préoccupations. Dès les débuts de la période pythagoricienne, l'apport babylonien permet des progrès décisifs. La maîtrise des questions du second degré aboutit à une construction rigoureuse du pentagone régulier. L'algorithme d'approximation des racines est repris et prend le nom d'anthyphérèse. Il est probablement à l'origine de la découverte de ce que les Grecs appellent les incommensurables et qui correspond à notre notion de nombre irrationnel.

Si rien n'indique avec certitude que la proportion entre la diagonale d'un carré et de son côté est à l'origine de la découverte des incommensurables, √2 joue néanmoins un rôle fondamental dans les recherches sur leur nature. Dans un premier temps, les Grecs remarquent que l'anthyphérèse fournit une suite de proportions rationnelles qui s'approche de plus en plus de celle recherchée, sans jamais l'atteindre : un comportement qui ne fait aucun sens pour un peuple qui imagine que toute proportion est rationnelle. Le paradoxe d'Achille et de la tortue est probablement une trace de cette époque où l'incommensurabilité est plus vécue comme un scandale logique qu'un savoir cohérent. La maîtrise de l'anthyphérèse a néanmoins lieu avant la fin du V^e siècle av. J.-C.. Au début du IV^e siècle av. J.-C., elle est non seulement comprise pour √2 mais déjà généralisée à d'autres racines carrées d'entiers par Théétète, un mathématicien contemporain de Platon.

Un autre cheminement est envisagé pour la première démonstration de l'irrationnalité de √2. Il se fonde sur une remarque arithmétique : Le double d'un carré parfait n'est jamais un carré parfait. La duplication du carré et cette remarque implique l'irrationalité de √2. Un historien spécialiste de cette période, O. Becker remarque que cette démonstration repose sur un résultat d'arithmétique élémentaire que les premiers pythagoriciens connaissent et qu'ils appellent le principe du pair et de l'impair. Ce qui est avéré est que cette démonstration date du V^e siècle av. J.-C. et qu'elle est consigné par Aristote qui précise : «  Ils prouvent que le diamètre du carré est incommensurable au côté en montrant que, si l'on admet qu'il lui est commensurable, un nombre impair serait égal à un pair. »

Un troisième raisonnement consiste à faire usage d'une descente infinie à l'aide d'une construction géométrique. Il date d'une période plus tardive que celle des pythagoriciens. Il suppose en effet une méthode de démonstration inexistante avant Eudoxe de Cnide, un mathématicien du IV^e siècle av. J.-C..

Vers le nombre √2

Richard Dedekind propose une construction rigoureuse des nombres réels à la fin du XIX^e siècle.

L'histoire de la racine de deux se confond alors avec celle de la racine carrée et plus généralement des irrationnels. Elle peut se résumer en quelques lignes :

Les Grecs conçoivent ce que nous appelons les rationnels ou les réels comme des proportions, et non pas des nombres. La faiblesse des concepts apparaît dans une égalité comme : √2 x √3 = √6. Pour les Grecs, elle n'est pas démontrable ; √2 x √3 désigne une proportion entre aires et √6 n'a pas de sens dans le monde des aires. Le carré d'une surface n'existe pas chez les grecs.

La culture mathématique arabe de l'antiquité est à l'origine du prochain progrès. Au début du IX^e siècle, le perse Al-Khawarizmi développe les concepts d'équation et d'inconnue. Ces découvertes, parfois considérées comme la naissance de l'algèbre, amènent petit à petit l'idée de donner un statut de nombre aux fractions puis aux proportions incommensurables. Les propriétés algébriques des racines carrées sont établies. Omar Khayyam développe au XI^e siècle une théorie où les proportions sont des nombres, même si les incommensurables sont encore considérées comme impropres. L'Europe n'assimile ces notions que tardivement, le XVI^e siècle est une période de polémique pour savoir si les incommensurables méritent le statut de nombre. C'est à cette époque que l'usage du symbole √ se répand.

Construire un univers de nombres où l'égalité √2 x √3 = √6 est démontrée rigoureusement n'est pas simple. Cette construction n'apparaîtra que tardivement ; en 1876 Dedekind résout cette question.