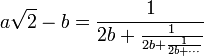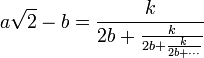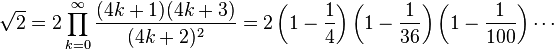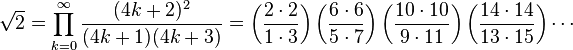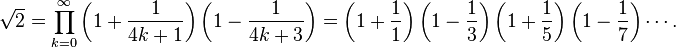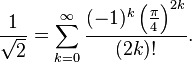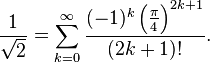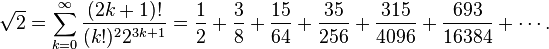Racine carrée de deux - Définition

Autres propriétés

Normalité

La normalité est un concept se basant sur la distribution des chiffres du développement décimal d’un nombre irrationnel, à savoir si tous les chiffres de 0 à 9 apparaissent dans ce développement et avec la même fréquence. En ce qui concerne √2, on ignore s’il est normal dans le système décimal ou dans toute autre base de numération.

Degré algébrique et degré d'irrationalité

est un nombre algébrique de degré 2, dit entier quadratique, car solution de l’équation polynômiale du second degré à coefficients entiers x² − 2 = 0 et de monôme dominant de coefficient égal à un, mais d’aucune de degré 1 de par son irrationalité. On sait ainsi qu’il est difficilement approchable par une suite rationnelle p_n/q_n ; l’erreur est en mieux en

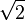
|√2 − p_n/q_n| ~ 1/q_n².

Comme pour tout nombre algébrique irrationnel, son degré d’irrationalité est 2.

Développement en fraction continue

√2 est relié à un certain nombre de développements en fractions continues périodiques, par propriété des entiers quadratiques.

√2 est relié au développement en fraction continue suivant

pour 2a² − b² = 1, (a, b) entiers strictement positifs. On notera ce développement de manière plus concise :

a√2 − b = [0; 2b, 2b, 2b, …]

On en tire les valeurs suivantes de √2 :

√2 = [1; 2, 2, 2, …].

√2 = 1/5 × [7; 14, 14, 14, …]

√2 = 1/29 × [41; 82, 82, 82, …]

Plus généralement, se relie à la fraction continue généralisée suivante :

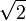
notée sous forme plus concise

a√2 − b = [0; k, 2b; k, 2b; k, 2b; …]

avec k = 2a² − b², et (a, b) entiers strictement positifs. On en déduit les quelques développements de suivants :

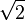
√2 = 1/2 × [3; -1, 6; -1, 6; -1, 6; …]

√2 = 1/12 × [17; -1, 34; -1, 34, -1, 34; …]

√2 = 1/70 × [90; -1, 180; -1, 180, -1, 180; …]

Éléments de démonstration : soit la suite (u_n) définie par la relation de récurrence u_{n + 1} = −k/(2b + u_n) et ε_n = |u_n − (a√2 − b)|. Alors on peut montrer que ε_{n + 1} < Kε_n, avec 1/|1 + 2b/(a√2 − b)| < K < 1 dans un voisinage de a√2 − b.

Développements en série et produit infini

Produits infinis

L’identité cos(π/4) = sin(π/4) = 1/√2 et la représentation en produit infini du sinus et du cosinus mènent aux développements suivants

Le dernier produit peut s’écrire de manière équivalente :

Séries

Le nombre peut aussi être évalué sous forme de série en utilisant le développement de Taylor d’une fonction trigonométrique en  :

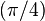
On peut aussi utiliser la fonction en 1 :

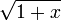
La convergence de la dernière série peut être accélérée par le biais d’une transformation d’Euler pour donner :