Racine carrée de deux - Définition
La liste des auteurs de cet article est disponible ici.
Constructions et démonstrations grecques
Construction de √2 à la règle et au compas
Comme toutes les racines carrées de nombre entier, √2 est constructible à la règle et au compas ; a contrario, ce n’est pas le cas de la racine cubique de 2, par exemple.
Étant donné un segment AB de longueur unité, voici les différentes étapes pour construire un segment de longueur √2 avec une règle non graduée et un compas :
- Tracer le symétrique B′ de B par rapport à A
- Tracer le cercle C1 de centre A et de rayon AB, il coupe la demi-droite ]BA) en B′
- Tracer la médiatrice (AH) de [BB′]
- Tracer le cercle C2 de centre B et de rayon r > AB
- Tracer le cercle C3 de centre B′ et de rayon r, il coupe C2 en deux points, H et H′
- Tracer le segment [AH] il intersecte C1 en un point C.
À cette étape le segment [BC] de longueur √2 est construit. Comme tout nombre constructible à la règle et au compas, √2 est constructible au compas seul.
Les étapes d’une construction possible sont :
- Tracer quatre sommets consécutifs B, G, H, I de l’hexagone régulier de centre A et de sommet B ; ceci permet de construire √3, l’unité étant la longueur AB.
- Tracer le cercle C1 de centre A et de rayon AB ;
- Tracer le cercle C2 de centre B et de rayon AB, il coupe C1 en deux points, soit G l’un d’entre eux ;
- Tracer le cercle C3 de centre G et de rayon AB, il coupe C1 en B et H ;
- Tracer le cercle C4 de centre H et de rayon AB, il coupe C1 en G et I ;
- Construire un triangle rectangle ABC d’hypoténuse BC = √3 (AB = 1) ; C est l’un des deux points tel que IC = IG et BC = BH (sachant que IG = BH = √3 > IB/2 = 1).
- Tracer le cercle C5 de centre I et de rayon IG ;
- Tracer le cercle C6 de centre B et de rayon BH (= IG), il coupe C5 en C.
À cette étape le segment [AC] de longueur √2 est construit.
.
Irrationalité
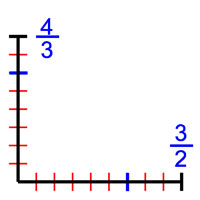
Si les Grecs héritent des méthodes des Babyloniens, elles s'insèrent dans un monde différent, essentiellement géométrique. Ils imaginent dans un premier temps que toutes les longueurs sont des fractions. Ils en déduisent qu'il suffit de choisir adroitement l'unité de longueur pour que les grandeurs présentes dans une figure correspondent à des nombres entiers. Ainsi, si à l'image de la figure de droite ils ont affaire à deux longueurs 3/2 et 4/3 avec la première unité de longueur (en bleu), ils choisissent comme unité de longueur le sixième de la précédente (en rouge), 3/2 devient 9 et 4/3 devient 8.
Avec cette logique, une question naturelle est celle des entiers caractérisant un demi-carré c'est à dire mesurant la diagonale et le côté d'un carré. Ces entiers n'existent pas, c'est à dire qu'il n'existe aucune unité de longueur tel que le côté et la diagonale s'obtiennent par multiplication de l'unité de longueur avec des entiers. Les grecs disent dans ce cas que la proportion entre la diagonale et le côté ou que les longueurs de la diagonale et du côté sont incommensurables. Dans notre langage, cette proportion est un nombre égal à √2, si ce nombre était commensurable, il s'écrirait p.u/q.u, où p, q sont des nombres entiers et u est un nombre quelconque représentant l'unité. En simplifiant par u, le nombre devient p/q, autrement dit un nombre rationnel. Ainsi, l'incommensurabilité d'une proportion est équivalente à notre notion d'irrationnel.
La fusion de la culture babylonienne, que van der Waerden qualifie d'algébrique, avec la culture géométrique grecque est à l'origine d'une nouvelle démarche mathématique, appelée algèbre géométrique. Cette démarche permet de démontrer l'irrationnalité de √2.
Le pair et l'impair
Une des démonstrations candidate pour être la plus ancienne est par l'absurde. Elle se fonde sur un principe que les pythagoriciens appellent le pair et l'impair. Ce principe indique que le carré d'un nombre pair est pair et le carré d'un nombre impair est impair.
On suppose qu'il existe une unité telle que la diagonale et le côté d'un carré sont des longueurs entières. On choisit la plus grande de ces unités, on note p la longueur de la diagonale et q celle du côté. La duplication du carré montre que p2 = 2q2, ce qui montre que p2 est pair et donc p l'est aussi. On en déduit que q est impair car sinon le double de l'unité permettrait d'exprimer la diagonale et le côté comme des entiers, ce qui contredit le fait que celle choisie est la plus grande de toutes. Le graphique à gauche montre que le carré de côté q est d'aire égale au rectangle en bleu de base p/2 et de hauteur p. Ce rectangle se divise en deux carrés de côté p/2, car p est un nombre pair. On en déduit que le carré de q est pair et donc que q l'est aussi. Le nombre q est à la fois pair et impair, cette contradiction termine la démonstration.
Il existe aussi des versions plus expéditives de cette démonstration, faisant usage d'un savoir plus grand sur les fractions de nombres entiers.
On suppose par l’absurde que la racine carrée de 2 est rationnelle. Dans ce cas on pourrait écrire √2 sous forme de fraction irréductible, c’est-à-dire que p et q n’auraient pas de facteurs premiers communs. Il en serait donc de même pour p² et q², ce qui signifierait que p²/q² serait une fraction sous sa forme irréductible. Une telle forme étant unique, l’égalité p²/q² = 2/1 entraînerait p² = 2 et q² = 1. La première de ces deux égalités est impossible pour p entier ; on a donc abouti à une contradiction.
Descente infinie
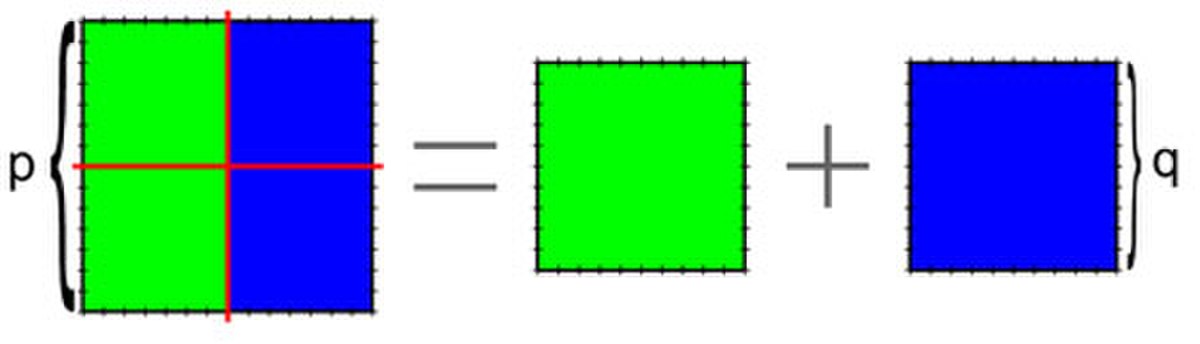
La démonstration présentée dans ce paragraphe est nécessairement plus tardive. Elle se fonde sur le principe de la descente infinie et sur l'égalité (√2 + 1)(√2 - 1) = 1. Pour les Grecs, une telle égalité n'a pas de sens, √2 n'est pas un nombre. En revanche, si p est la longueur d'une diagonale et q celle d'un côté d'un carré, elle se traduit directement par : (p + q)(p - q) = q2. Elle devient une égalité entre l'aire d'un carré et celle d'un rectangle de base la somme d'une diagonale et d'un côté, et de hauteur la différence d'une diagonale et d'un côté d'un carré. Sous forme de proportion, on obtient :
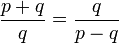
Si le côté et la diagonale d'un carré sont commensurables, cela signifie qu'il existe une unité de longueur telle que p et q soient des entiers. En retirant 1 à cette double expression de la même fraction, on obtient :
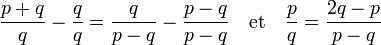
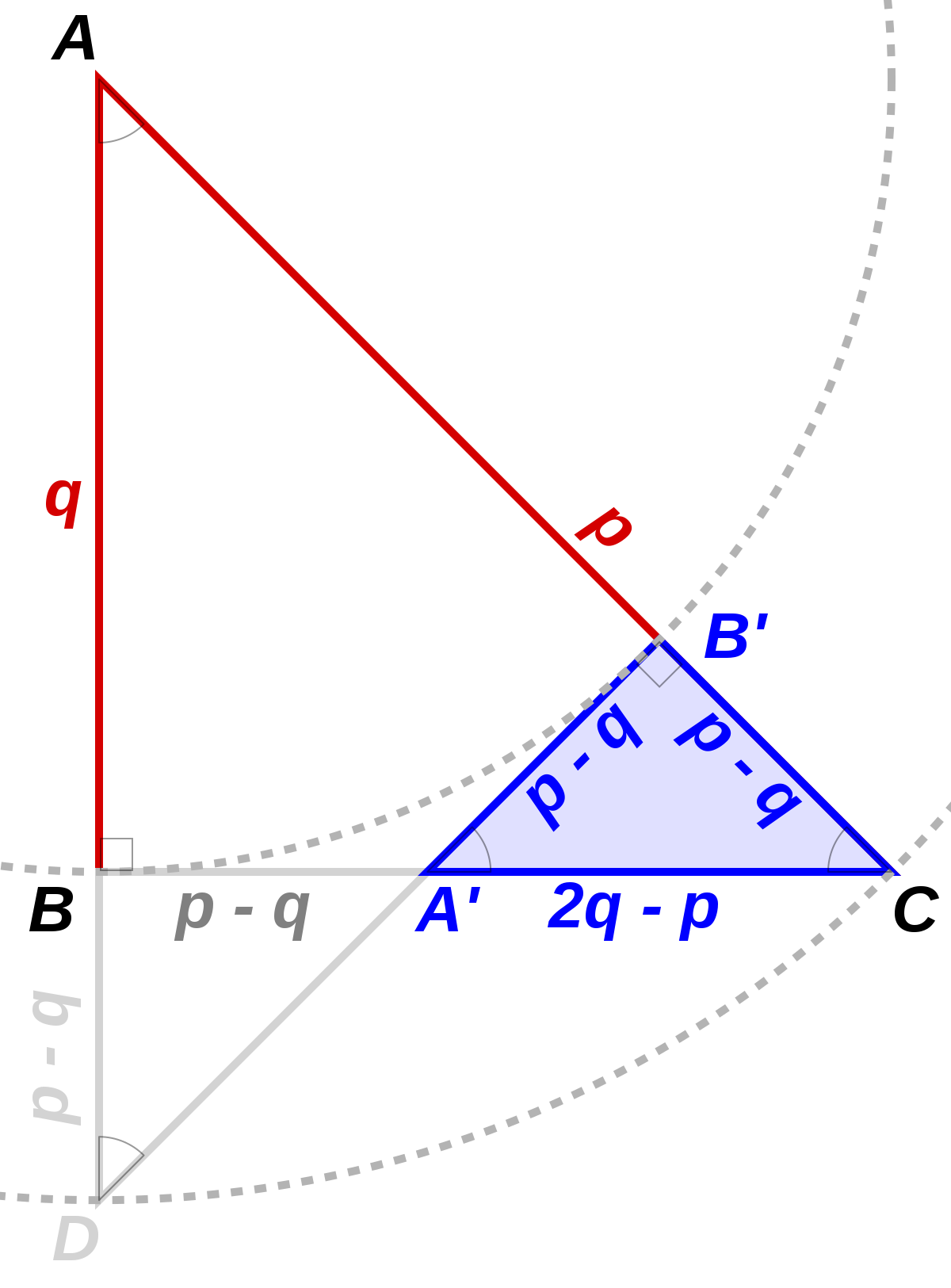
Cette dernière égalité et le théorème de Thales indique que le triangle ABC de la figure de droite est semblable à A'B'C. On obtient un nouveau triangle rectangle isocèle avec des côtés entiers, plus petits que les précédents. En réitérant le processus, on obtient des triangles rectangles isocèles de plus en plus petits et ayant des côtés entiers. Leurs bases forment une suite d'entiers positifs strictement décroissante et infinie, ce qui est absurde.
On peut terminer plus rapidement la démonstration en supposant que l'unité est choisie la plus grande possible, ce qui revient à dire qu'avec cette convention, le triangle rectangle isocèle d'hypoténuse p et de cathète q est le plus petit possible avec des côtés entiers. La contradiction provient du fait que le triangle isocèle de base 2q - p et de côtés p - q possèdent aussi des côtés entiers et est rectangle, mais en plus il est plus petit. Avec notre langage algébrique, cette contradiction s'exprime de la manière suivante : si q est le plus petit entier tel que q√2 est entier, qui existe si √2 est rationnel, alors q√2 - q possède la même propriété et est pourtant plus petit.
Il est possible de montrer que le triangle A'B'C est rectangle, sans l'usage de l'algèbre géométrique importée des babyloniens.
On construit la bissectrice intérieure de l'angle
Le quadrilatère ABA′B′ est symétrique par rapport à sa diagonale (AA′) ; on en déduit d'une part que son angle en B′ est égal à son angle en B donc droit, et d'autre part que la longueur AB′ est égale à AB donc à q.
On s'intéresse alors au triangle A′B′C. Son angle en B′ est droit (comme supplémentaire de l'angle droit
Les longueurs des côtés de ce triangle sont entières, en effet :
-
- B′C = AC - AB′ = p - q,
- B′A′ vaut aussi p - q (le triangle est isocèle). Vu la symétrie du quadrilatère ABA′B′ on obtient également BA′ = p - q
- A′C = BC - BA′ = q - (p - q) = 2q - p.
Fraction continue
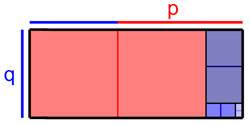
Une autre candidate pour être la première démonstration de l'irrationnalité de √2, met encore plus en valeur l'apport des Babyloniens et l'interprétation géométrique qu'en font les Grecs. On utilise encore les mêmes notations, p désigne la longueur de la diagonale et q du côté d'un carré. Cette fois, le raisonnement est direct et les longueurs p et q ne sont plus supposées entières. On construit un rectangle de base p + q et de hauteur q. La proportion p + q / q, égale à 1 + √2 est appelée proportion d'argent. Elle dispose de propriétés analogue à la proportion d'or.
L'objectif est de remplir le rectangle de carrés de côté le plus vaste possible, exactement comme pour une multiplication babylonienne. Le plus grand côté possible pour les premiers carrés est q, car la hauteur est égal à q. Comme p + q est plus grand que 2.q et strictement plus petit que 3q, on peut construire deux carrés de côté q, en rouge sur la figure. La zone restante (en bleu sur la figure) est un rectangle de côté q et p - q. Or on dispose de la formule :
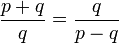
Elle indique que le rectangle initial et le bleu sont semblables, la proportion entre les deux étant le rapport p + q / q. Il est alors possible de remplir la zone restante d'exactement deux carrés de taille maximale, comme précédemment et la zone restante est encore un rectangle semblable à l'initial. Finalement on obtient 2 carrés de côté q, puis 2 carrés de côté (p + q) / q fois plus petits que les premiers, puis 2 carrés de côté (p + q) / q fois plus petits que les précédents et la suite ne s'arrête jamais.
Dans le cas de grandeurs commensurables le comportement est différent. Il existe alors une unité telle que la longueur de la base et celle de la hauteur soient des entiers. Avec cette unité, les côtés des différents carrés sont toujours des entiers, ce qui garantit que la suite finit par s'arrêter, car les carrés ne peuvent devenir infiniment petits. Ainsi une fraction a/b est entière, si et seulement si la suite construite précédemment s'arrête. Cet algorithme, initialement conçu comme une manière de trouver une commune mesure entre deux longueurs entières, est présent chez Euclide, mais il devient une méthode pour déterminer son équivalent arithmétique, c'est à dire le PGCD de deux entiers. Ce critère n'est pas rempli pour la proportion p/q, cette proportion n'est pas rationnelle.
La construction de la suite 2, 2, 2, ... s'appelle pour les Grecs une anthyphérèse et maintenant la fraction continue de la proportion d'argent. Pour Maurice Caveing, cette anthyphérèse est probablement la première preuve complète de l'irrationnalité de √2. D'autres arguments convainquent le spécialiste Árpád Szabó du fait que cette démonstration serait aussi la première. Vu sous un angle plus algébrique, la suite 2, 2, 2, correspond exactement à la méthode de calcul babylonienne et porte le nom de dunámeis ou δυνάμεών chez les Grecs. Ce terme est ancien et se retrouve chez les Éléates, la première démonstration daterait de leur époque, qui est aussi celle des paradoxes de Zénon. Il est néanmoins peu probable qu'elle disposait originellement de la forme aboutie présentée ici.
On considère ici le même développement, mais sur un rectangle de base √2 et de hauteur 1. Le premier carré correspond à la partie entière de √2 et la première égalité s'écrit √2 = 1 + (√2 - 1). En négligeant la partie fractionnaire, on obtient une première approximation 1 déjà trouvée avec la méthode babylonienne. On peut encore écrire ce résultat sous la forme :
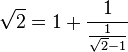
Les dimensions 1 et √2 - 1 correspondent au carré bleu ainsi qu'aux numérateur et dénominateur de la fraction 1/(√2 - 1). Une fois encore, les carrés bleus foncés correspondent à la partie entière de cette fraction. En multipliant au numérateur et au dénominateur par √2 + 1, on obtient la nouvelle fraction (√2 + 1)/1. La partie entière est donc encore 2 et l'on obtient l'égalité :
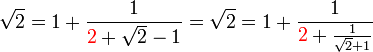
En négligeant le terme √2 - 1, on obtient la valeur 3/2 = 1,5 soit la deuxième approximation déjà trouvée avec la méthode babylonienne. Le même raisonnement permet maintenant de prendre en compte les carrés bleus plus clairs et l'on obtient l'approximation :
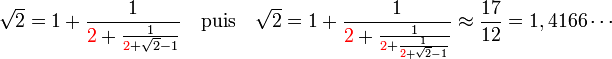
Une fois encore on obtient l'approximation des babyloniens. Cette présentation est juste une interprétation géométrique différente du même algorithme. Chez les babyloniens, il est connu comme une méthode d'approximation de √2, dans le livre X des Éléments d'Euclide c'est une méthode, nommée anthyphérèse, pour évaluer une incommensurabilité.