Représentations du groupe des quaternions - Définition
La liste des auteurs de cet article est disponible ici.
Représentation sur le corps des complexes
Caractères irréductibles
Le quotient de Q8 par C2 est un groupe abélien isomorphe à V. Cette remarque détermine quatre caractères irréductibles correspondant à des représentations de degré un. En effet, si χ désigne un caractère de degré un de V et φ le morphisme surjectif canonique de Q8 dans V alors χoφ est une représentation de degré un de Q8 et donc un caractère irréductible. On note ici χ1 le caractère de la représentation triviale et χX le caractère égal à -1 sur X désignant ici une des classes de conjugaison A, B ou AB et 1 ailleurs.
Le nombre de représentations irréductibles à un isomorphisme près est égal au nombre de classes de conjugaison. Il ne reste donc qu'une unique représentation irréductible ρ à trouver et son caractère associé, noté ici χρ. L'image de l'élément 1 du groupe par χρ est égal à deux et représente le degré de la représentation ρ. Pour s'en convaincre il suffit de remarquer que la somme des carrés des degrés des différentes représentations irréductibles du groupe est égal à son ordre. χρ est de norme égal à 1 et est orthogonal aux autres caractères irréductibles. Ces considérations déterminent intégralement le dernier caractère. Résumons ces résultats dans une table :
|
Représentation irréductible de degré deux
Une méthode rapide pour déterminer la dernière représentation est donnée par les représentations induites. Pour obtenir directement une représentation de degré deux, il est nécessaire de considérer un sous-groupe H d'ordre quatre. Définissons H comme le groupe isomorphe à C4 engendré par a. Une représentation θ doit alors être choisie pour être ensuite induite sur Q8. Cette représentation θ doit être choisie de telle manière à ce que la représentation induite ρ soit de caractère orthogonale avec les représentations de degré 1. La loi de réciprocité de Frobenius permet simplement de vérifier cette orthogonalité. Elle s'exprime de la manière suivante :

Sur 1 et -1 tous les cararactères des représentations de degré 1 sont égaux à 1. Sur a et -a, ils valent soit 1 soit -1. Si l'on choisit pour caractère celui qui à a associe i, alors les orthogonalités recherchées sont bien obtenues. L'utilisation du critère d'irréductibilité de Mackey et la remarque que tous les automorphismes intérieurs laissent les éléments du groupe invariant permet de conclure sans calcul. Et la représentation ρ est bien la représentation induite de θ.
Pour connaitre cette représentation, il suffit de déterminer les matrices de a et de b car ils sont générateurs du groupe. Si Ma désigne la matrice de a et Mb celle de b, on obtient :
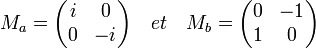
Algèbre semi-simple
Dans le cas des complexes, on remarque que les quatre matrices M1, Ma, Mb ,Mab forment une base des matrices 2x2. En effet :
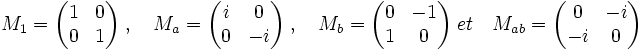
Si Mc désigne la matrice de l'élément c de C[Q8], l'algèbre C[Q8] vérifie l'égalité :
![\forall c \in \mathbb C[Q_8] \quad \exists ! (a_i)_{i \in [1,8]} \in \mathbb C^8 \quad M_c = \begin{pmatrix} a_1 & 0 & 0 & 0 & 0 & 0 \\ 0 & a_2 & 0 & 0 & 0 & 0 \\ 0 & 0 & a_3 & 0 & 0 & 0 \\ 0 & 0 & 0 & a_4 & 0 & 0 \\ 0 & 0 & 0 & 0 & a_5 & a_7 \\ 0 & 0 & 0 & 0 & a_6 & a_8 \end{pmatrix}](https://static.techno-science.net/illustration/Definitions/autres/e/ef7320aaef2811c73ffe2b45046aafa1_222e370e3662b80a550d3fd8b8497c0a.png)
Son centre est bien égal à C5 et est isomorphe à l'ensemble des fonctions centrales.

















































