Représentations du groupe symétrique d'indice quatre - Définition

Introduction

En mathématiques les représentations du groupe symétrique d'indice quatre noté S₄ sont un exemple d'application de la théorie des représentations d'un groupe fini.

Sur le corps des nombres complexes, il existe cinq représentations irréductibles du groupe symétrique d'indice quatre, la représentation triviale, celle correspondant à la signature, une d'ordre deux et deux d'ordre trois. L'une s'obtient de l'autre par produit tensoriel avec la représentation correspondant à la signature. Une des représentations de degré trois correspond aux rotations linéaires laissant invariant un cube.

L'analyse des représentations de S₄ est une illustration des concepts comme le théorème de Maschke, les caractères, la représentation régulière, les représentations induites et la réciprocité de Frobenius.

Histoire

L'histoire des représentations du groupe symétrique d'indice quatre, avec celui d'ordre cinq et des groupes alternés associé joue un rôle particulier pour la théorie des caractères. Le 12 avril 1896 est la date de naissance généralement considérée de cette théorie. Dans une série de lettres adressées à Dedekind , Frobenius analyse les représentations des groupes cités et présente les fondements qu'il développe pendant les années à venir.

Si les méthodes sont différentes de celles maintenant utilisées, Frobenius utilise en effet comme outil essentiel les déterminants de groupes tombés maintenant en désuétude, les bases de la théorie sont esquissées. Elle se développe rapidement, Heinrich Maschke démontre le théorème portant maintenant son nom trois ans plus tard. En 1911, William Burnside publie la seconde édition du livre encore de référence contenant toutes les techniques utilisées dans cet article.

Représentation

L'objectif du paragraphe est la détermination effective des différentes représentations. Pour celle de dimension un, c’est-à-dire t et σ, elles se confondent avec leur caractère, elles sont donc de facto déterminées.

Le groupe S₄ est engendré par les transpositions, il n'est donc nécessaire que de déterminer les représentations que pour elles. De plus, on remarque que les transpositions (12), (23), (34) engendrent toutes les transpositions, donc le groupe entier. Dans la suite de paragraphe, les représentations ne sont exprimées que sur ces trois éléments. Les autres se déduisent par produits des automorphismes précédents.

Représentation de θ

Représentation de S₃ comme groupe des isométries du triangle

Considérons le groupe H formé des quatre éléments 1 et les trois éléments de la classe de conjugaison de la forme (ab)(cd). On vérifie aisément que c'est un sous groupe, de plus comme il est formé par l'union de deux classes de conjugaison, il est distingué. Considérons alors le groupe S₄/H. C'est un groupe d'ordre six, isomorphe à S₃. Soient s la surjection canonique de S₄ dans S₄/H et (W, θ₂) la représentation irréductible de S₃ d'ordre deux (cf Représentations du groupe symétrique d'ordre trois), définissons alors θ comme étant égal à θ₂os. La composition de morphismes étant un morphisme, (W, θ) est une représentation. Déterminons son caractère : il existe trois transpositions dans S₃ correspondant à douze valeurs dans S₄, à savoir les transpositions et les permutations circulaires du type (abcd). Il existe deux éléments d'ordre trois dans S₃ correspondant à la classe (abc) dans S₄, enfin la classe de l'élément neutre est composé du sous-groupe H. On en déduit que cette représentation possède bien le caractère recherchée et :

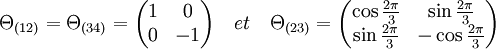
La représentation possède bien le caractère recherché. Elle est de degré deux, le caractère est donc bien égal à deux pour la classe de conjugaison associée à l'identité, composée par le groupe H. Les transpositions représentent trois images par la représentation, chaque classe contient deux transpositions et deux cycles d'ordre quatre, la valeur associée au caractère est égale à zéro. Enfin, les cycles d'ordre trois sont formés par les éléments de la classe (abc), elle engendre deux images par la représentation.

Représentation de S₄ comme groupe des isométries du triangle

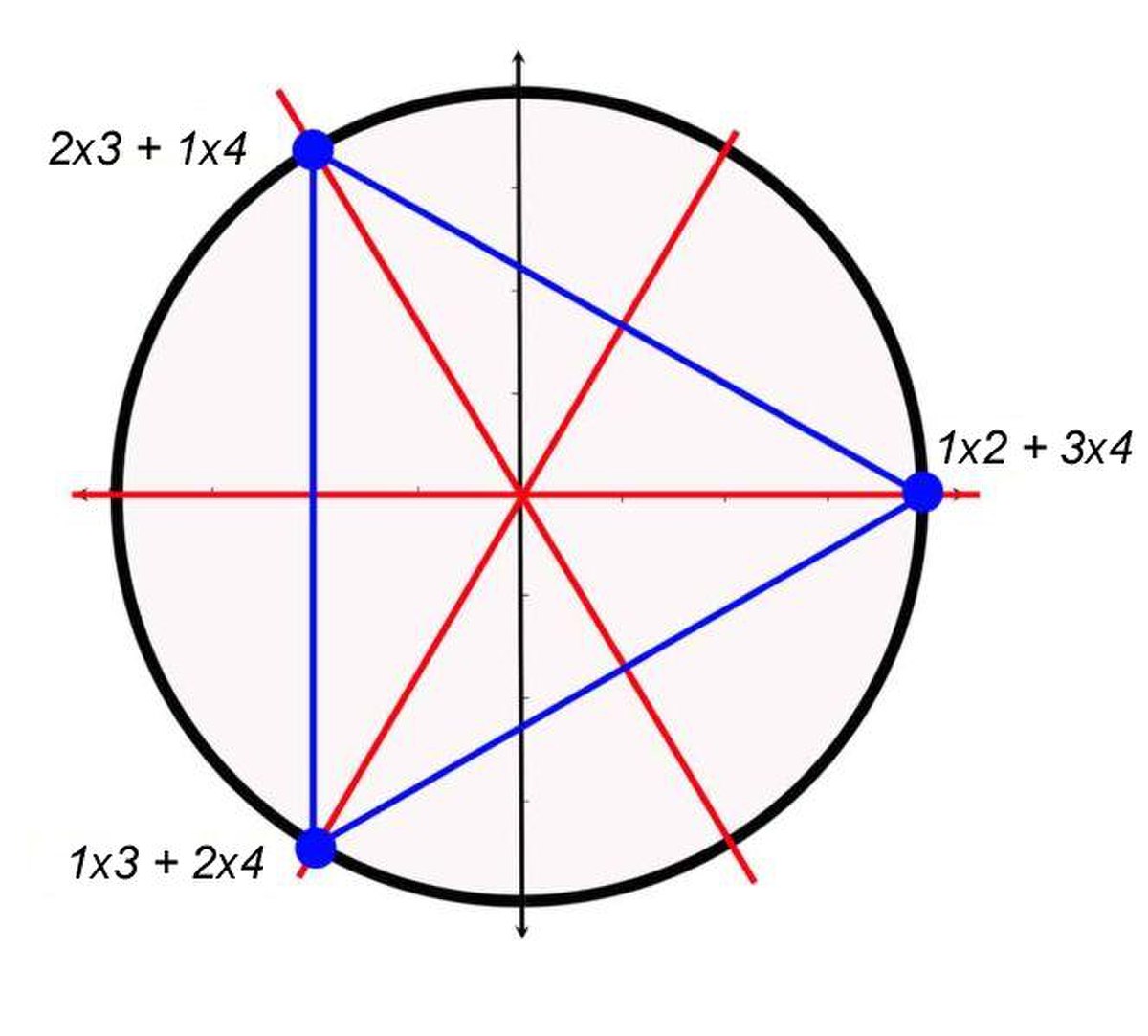
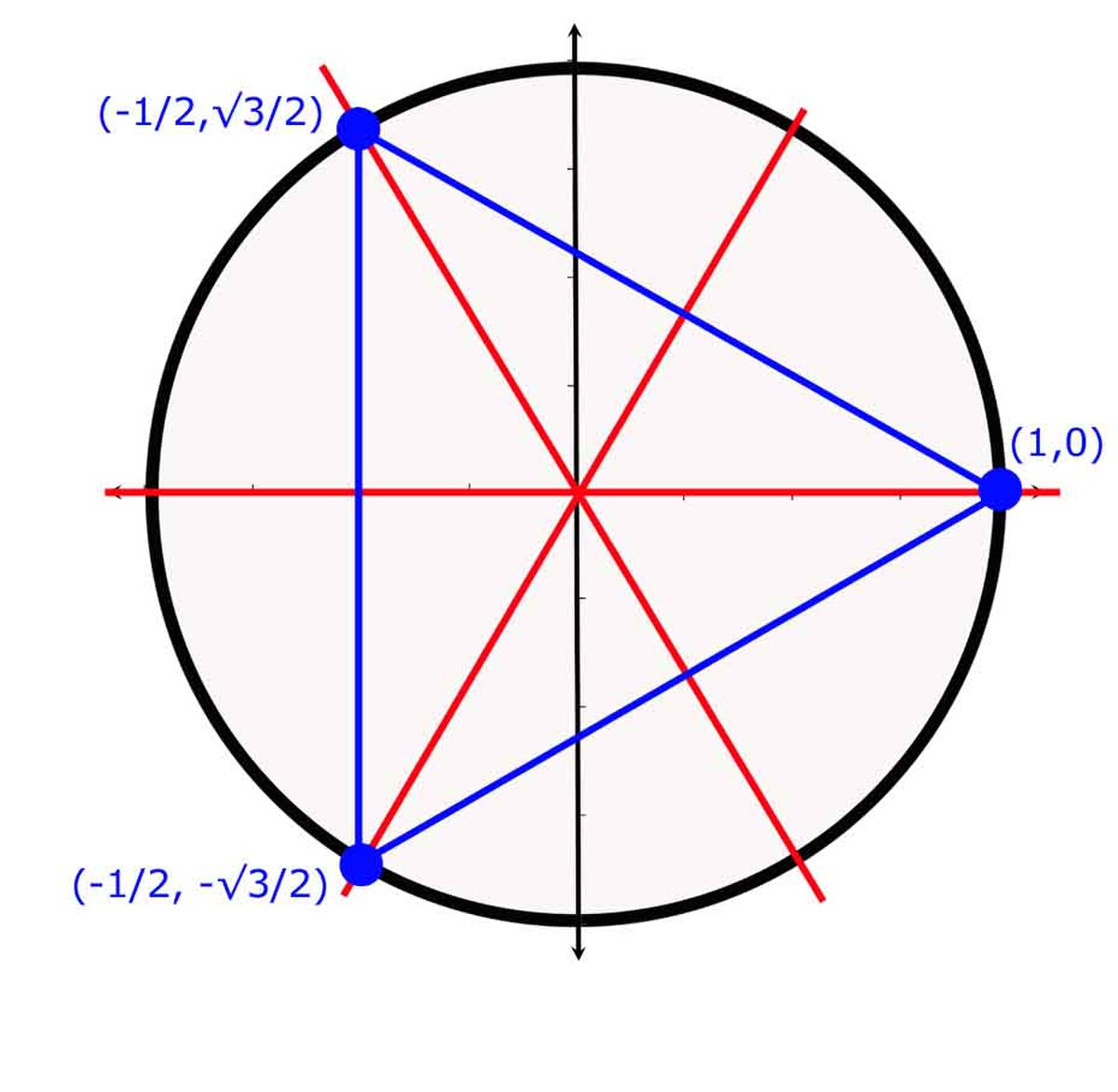
La représentation est alors celle du groupe des isométries du triangle. Elle n'est pas fidèle et chaque automorphisme de la représentation possède quatre antécédents. La figure de droite illustre cette représentation. On a nommé les trois sommets du triangle au moyen des trois étiquettes 1x2 + 3x4, 2x3 + 1x4 et 1x3 + 2x4. Une permutation de S₄ agit directement sur les chiffres de chaque étiquette. Ainsi,la transposition (12) laisse le sommet 1x2 + 3x4 invariant mais permute les deux sommets 2x3 + 1x4 et 1x3 + 2x4. On pourra vérifier que l'action de cette transposition est identique à celle de la transposition (34) ou celle des permutations circulaires (1324) ou (1423). Une telle action du groupe S₄ est utilisée pour résoudre les équations du quatrième degré.

Représentation de φ

Représentation de S₄ comme groupe des rotations du cube.

Considérons la représentation naturelle, celle définie par le fait que le groupe S₄ opère par permutation sur une base (e_i) d'un espace de dimension quatre. Le paragraphe précédent montre qu'une telle représentation possède le caractère de φ₁, obtenue en considérant un sous-espace stable par l'action de S₄, et supplémentaire de la droite engendrée par la somme des e_i.

Si l'on considére la base (u_i) définie par la matrice de passage P de (u_i) dans (e_i), on obtient comme matrice de la représentation φ₁ dans la base constituée des trois derniers vecteurs u_i :

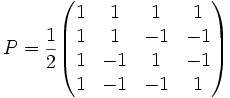
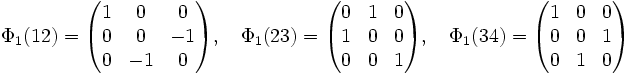
Les images par Φ₁ des permutations de S₄ sont alors les matrices orthogonales laissant globalement invariant le tétraèdre régulier de sommets M₁ = (-1,-1,-1), M₂ = (-1,1,1), M₃ = (1,-1,1) et M₄ = (1,1,-1), et permutant ces quatre sommets. Les transpositions (ab) correspondent à des réflexions, les permutations (ab)(cd) à des demi-tours, les permutations (abc) à des tiers de tour, et les permutations (abcd) aux composées d'un quart de tour et d'une réflexion.

Pour obtenir la représentation φ₂, il suffit de multiplier la représentation matricielle de φ₁ par le caractère σ. Elle est généralement obtenue avec les générateurs suivant:

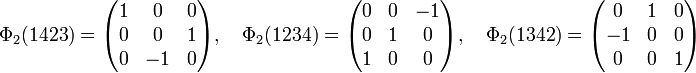
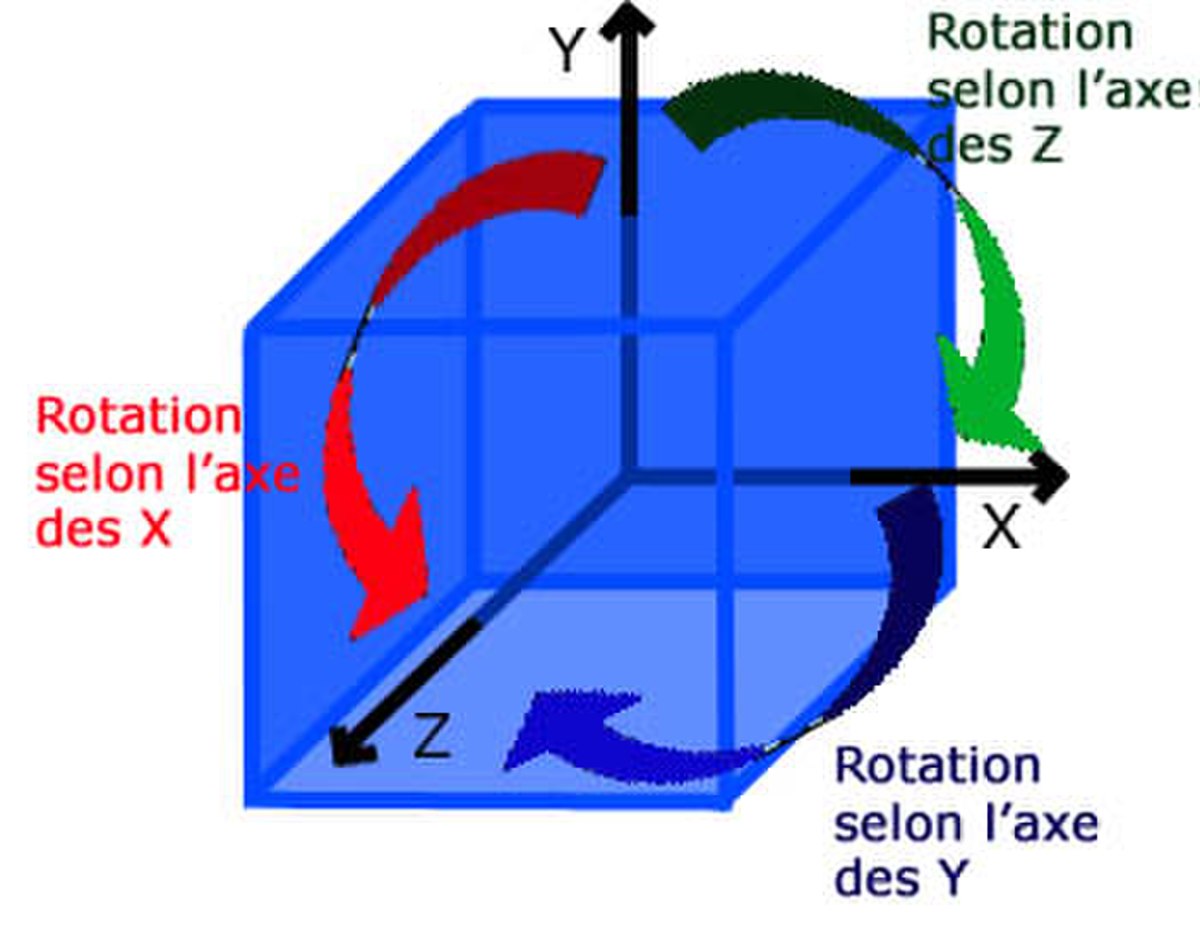
On reconnait trois rotations laissant invariant le cube, la première suivant l'axe des x, la deuxième suivant l'axe des y et la troisième suivant celui des z.

La figure au début du paragraphe illustre l'interprétation géométrique de la représentation φ₂, l'image de (1423) est celle représentée par la flèche rouge, celle de (1234) par la bleue et celle de (1342) par la verte. Les rotations du cube permutent alors les quatre diagonales du cube ou, de manière équivalente, les quatre paires de sommets opposés.

S₄ permute les couples de triangles opposés dans un cuboctaèdre

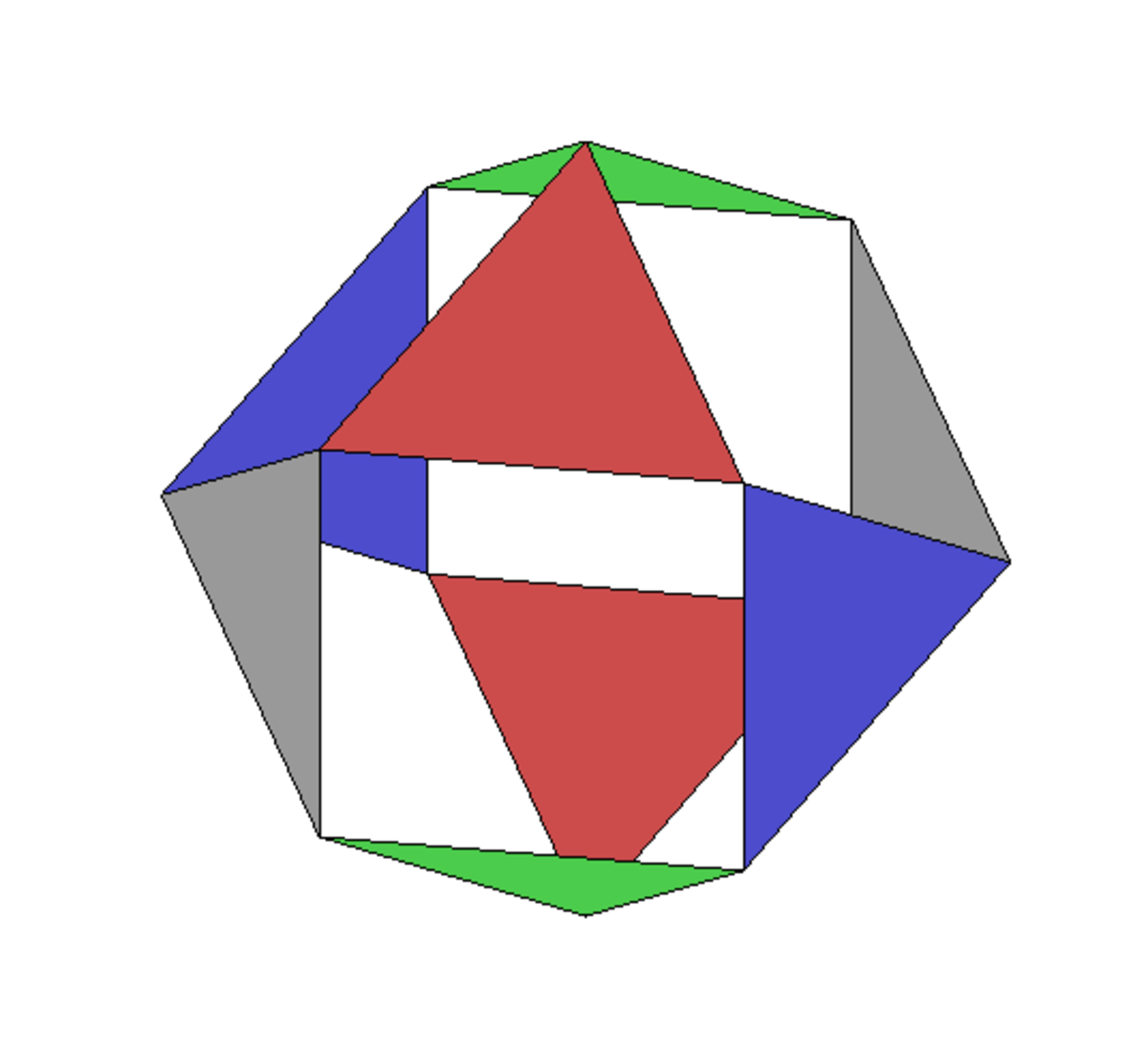
On peut également visualiser l'action de ces permutations de la façon suivante. Les rotations laissant invariant le cube laissent également invariant le cuboctaèdre. Les transpositions (ab) correspondent à des demi-tours d'axes passant par deux sommets opposés, les permutations (ab)(cd) à des demi-tours d'axes passant par les centres des carrés, les permutations (abc) à des tiers de tour d'axes passant par les centres des triangles, et les permutations (abcd) à des quarts de tour d'axes passant par les centres des carrés. Les rotations de la représentation permutent alors les quatre paires de triangles opposés.