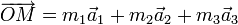Structure cristalline - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La structure cristalline (ou structure d'un cristal) est complètement décrite par les paramètres de son réseau de Bravais, son groupe d'espace et la position des atomes dans la maille. Ces atomes se répètent dans l'espace sous l'action des opérations de symétrie du groupe d'espace et forment ainsi la structure cristalline. Cette structure est un concept fondamental pour de nombreux domaines de la science et de la technologie.
Réseau cristallin
Un solide cristallin est constitué par la répétition périodique dans les 3 dimensions de l'espace d'un motif atomique ou moléculaire, appelé maille ; de la même façon qu'un papier peint est constitué de la répétition d'un même motif. La périodicité de la structure d'un cristal est donc représentée par un ensemble de points régulièrement disposés. Cet ensemble est appelé réseau cristallin et les points le constituant sont appelés nœuds du réseau.
À cause de la périodicité du réseau, toute paire de nœuds (O, M) définit un vecteur :
m1, m2, m3 étant des entiers relatifs.
Réseau de Bravais
Un réseau de Bravais est un réseau de nœuds obtenu par translation suivant des vecteurs de base à partir d'un nœud unique. Les réseaux de Bravais sont classés en 14 types en trois dimensions (5 types en deux dimensions) et représentent la périodicité de la structure cristalline. Celle-ci est obtenue à partir d'un ensemble minimal d'atomes occupant l'unité asymétrique, répétés dans l'espace selon les opérations du groupe d'espace du cristal. Tous les matériaux cristallins ont une périodicité correspondant à l'un de ces réseaux (mais pas les quasi-cristaux). Les 14 types de réseau de Bravais en trois dimensions sont listés dans le tableau ci-dessous.
| Système réticulaire | Types de réseaux | |||
| triclinique ou anortique | 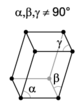
primitif (aP ) | |||
| monoclinique | 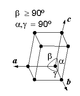
primitif (mP ) | 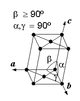
centré (mS ) | ||
| orthorhombique | 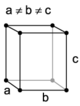
primitif (oP ) | 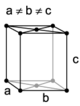
à base centrée (oS ) | 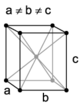
centré (oI ) | 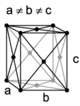
à faces centrées (oF ) |
| hexagonal | 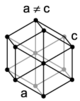
primitif (hP ) | |||
| rhomboédrique | 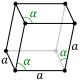
primitif | |||
| tétragonal (ou quadratique) | 
primitif (tP ) | 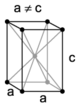
centré (tI ) | ||
| cubique (ou isométrique) | 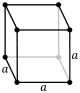
primitif (cP ) | 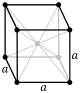
centré (cI ) | 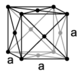
à faces centrées (cF ) | |
Maille élémentaire
Une maille élémentaire (ou primitive) est une maille de volume minimal qui contient un seul nœud du réseau. La répétition périodique de cette maille dans les trois dimensions de l'espace suffit à reproduire l'intégralité du réseau et de la structure. Souvent, pour des raisons de commodité ou pour faire mieux ressortir la symétrie, on utilise pour décrire le cristal une maille multiple, contenant plusieurs nœuds et qui n'est donc pas élémentaire.
Une maille élémentaire est définie par les 3 vecteurs a, b, c, linéairement indépendants. Le choix de ces 3 vecteurs n'est pas unique, on peut donc définir plusieurs mailles élémentaires qui pourront plus ou moins bien montrer la symétrie du réseau.