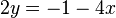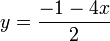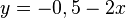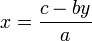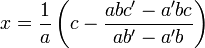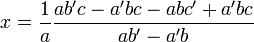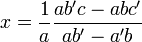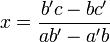Système d'équations (mathématiques élémentaires) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
Un système d'équations est un ensemble de plusieurs équations faisant appel aux mêmes inconnues.
Dans la vie courante et en sciences, les phénomènes dépendent le plus souvent de plusieurs paramètres. Pour les modéliser, on utilise en mathématiques les systèmes d'équations à plusieurs inconnues. Un problème mathématique comportant moins d'équations que d'inconnues a une infinité de solutions.
Exemple d'équation avec une infinité de solutions
L'équation
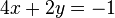

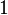
-
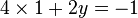
-
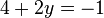
-
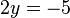
-
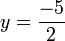
Plus généralement, si

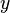
Systèmes de 2 équations linéaires à 2 inconnues
Interprétation graphique
Celle-ci va nous permettre d'établir des théorèmes utiles pour la suite.
Chaque équation du système
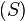
- les coordonnées du point d'intersection des deux droites représentent la solution de
- deux droites ont :
- soit un unique point d'intersection ;
- soit aucun point d'intersection ;
- soit une infinité de points d'intersection.
D'où le théorème suivant :
Théorème 1 : Un système de 2 équations linéaires à 2 inconnues a :
- soit une unique solution ;
- soit aucune solution ;
- soit une infinité de solutions.
On démontre aussi le théorème suivant (en se reportant plus haut pour les notations) :
Théorème 2 : Un système de 2 équations linéaires à 2 inconnues admet une seule solution si, et seulement si, le nombre
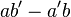
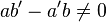
On appelle
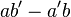
Exemple de résolution graphique : Soit le système :
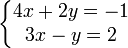
La première équation équivaut à
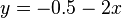
La deuxième équation équivaut à :
-
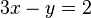
-
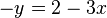
-
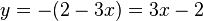
En traçant les droites d'équations respectives
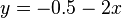
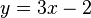
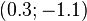
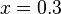
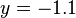
Résolution algébrique
Il existe deux méthodes a priori différentes, mais qui reposent sur le même principe de base : élimination d'une inconnue. Détaillons-les sur un exemple.
Méthode par substitution
Exemple : Reprenons le système :
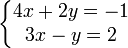
Exprimons
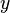

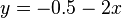
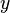
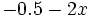
-
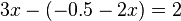
-
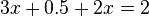
-
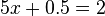
-
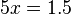
-
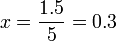
Or,
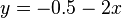
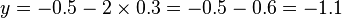
La solution du système est le couple
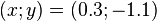
Méthode par combinaison ou élimination
Cette méthode est aussi appelée "méthode par addition" ou "par combinaison linéaire".
Exemple : Reprenons le système :
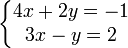
Pour éliminer
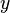
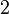
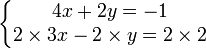
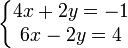
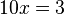
. En résolvant cette équation, on obtient
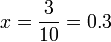
Remplaçons

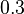
-
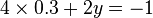
-
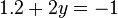
-
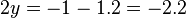
-
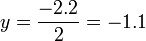
On retrouve la solution
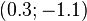
Cas général
D'une manière générale, pour un système sous la forme :
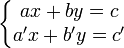
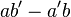
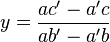
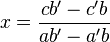
Le déterminant étant non nul, l'un au moins des coefficients a ou b est non nul. On peut, sans perdre de généralité, supposer que a est non nul. Sinon, on effectue un raisonnement analogue en divisant par b.
On a :
-
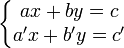
-
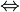
-
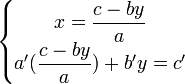
La première équation est donc :
Et la seconde équation donne :
- a'(c − by) + ab'y = ac' (en multipliant par a)
- a'c − a'by + ab'y = ac'
- y(ab' − a'b) = ac' − a'c
-
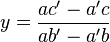
La première équation s'écrit alors :