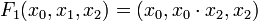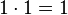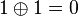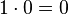Système dynamique séquentiel - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un système dynamique séquentiel (SDS, « sequential dynamical system » en anglais) est un formalisme décrivant la façon dont l'état des sommets d'un graphe change en fonction de leurs voisins, dans un ordre donné. Par exemple, un ensemble de personnes peut être représenté par un graphe, où chaque personne est un sommet et deux personnes sont connectées lorsqu'elles sont en contact. Dans un problème d'épidémie, l’état de ces personnes peut correspondre à leur état de santé : sains ou infectieux. Leur état de santé dépend de leurs voisins : un individu est infecté si un de ses voisins est infecté. Si l'état de santé est mis à jour dans un ordre, alors la propagation de cette épidémie se modélise par un système dynamique séquentiel. La notion d'ordre, ou de séquence, est une différence essentielle par rapport à des formalismes tels que les automates cellulaires, où l'application de fonctions selon les voisins se fait en parallèle (i.e., tous les états sont mis à jour en même temps). Le but de ce formalisme est d'étudier les transitions entre les différents états possibles du système, c'est-à-dire l'espace des phases, selon le graphe, les fonctions, et l'ordre.
Définition
Un système dynamique séquentiel (SDS) repose sur un graphe fini G, c'est-à-dire un ensemble de sommets pouvant être connectés deux à deux par des arêtes. Chacun des sommets de ce graphe a un état, dans l'ensemble fini K. De plus, il existe pour chaque sommet
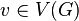
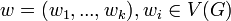
![[F_G,w] : K^n \rightarrow K^n](https://static.techno-science.net/illustration/Definitions/autres/2/2a96a513b65f341a4f7542085b1fe018_38d44a75b853bfc3985a8cd3a17f687b.png)
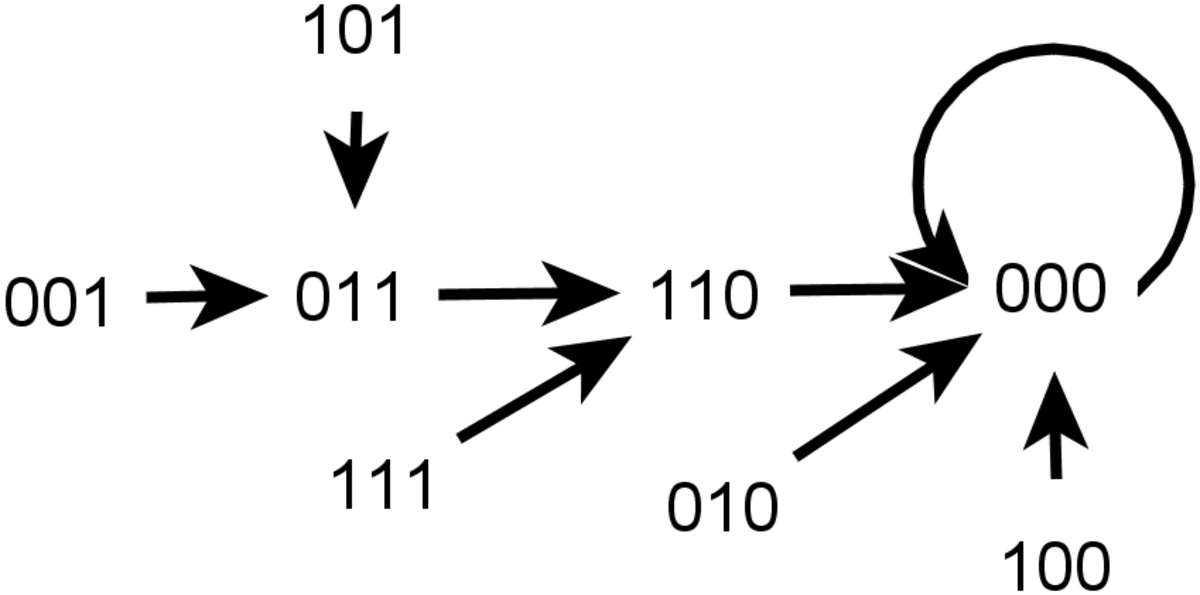
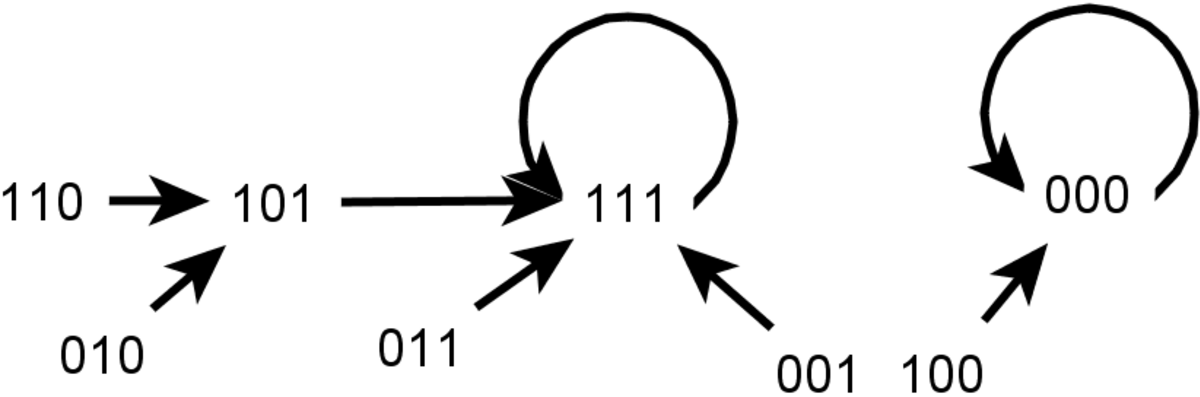
Espace des phases
L'espace des phases décrit les transitions entre les différents états possibles du système. Il s'agit donc d'un graphe, où un sommet correspond à un état possible, et un arc va d'un sommet à un autre s'il existe une transition entre les deux états. Formellement, l'espace des phases est le graphe dirigé Γ. Chaque sommet ayant un état parmi K possibles, l'ensemble des états correspond à toutes les combinaisons possibles d'états initiaux des n sommets. Ainsi,
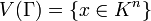
) | x \in V(\Gamma)\}](https://static.techno-science.net/illustration/Definitions/autres/1/1df7688dbd3ce0f42f4d2dc79a56c959_d38abdd8e6529aff592eca95f7dcefb1.png)
Exemple : réseau booléen
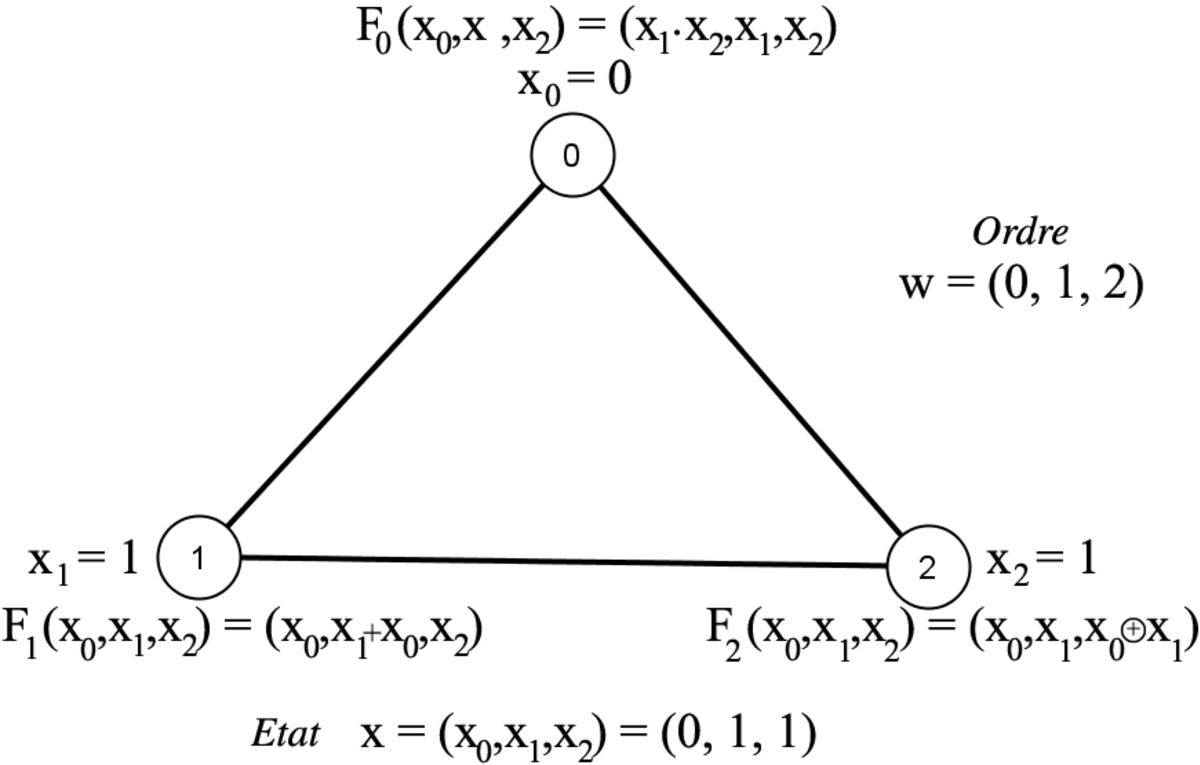
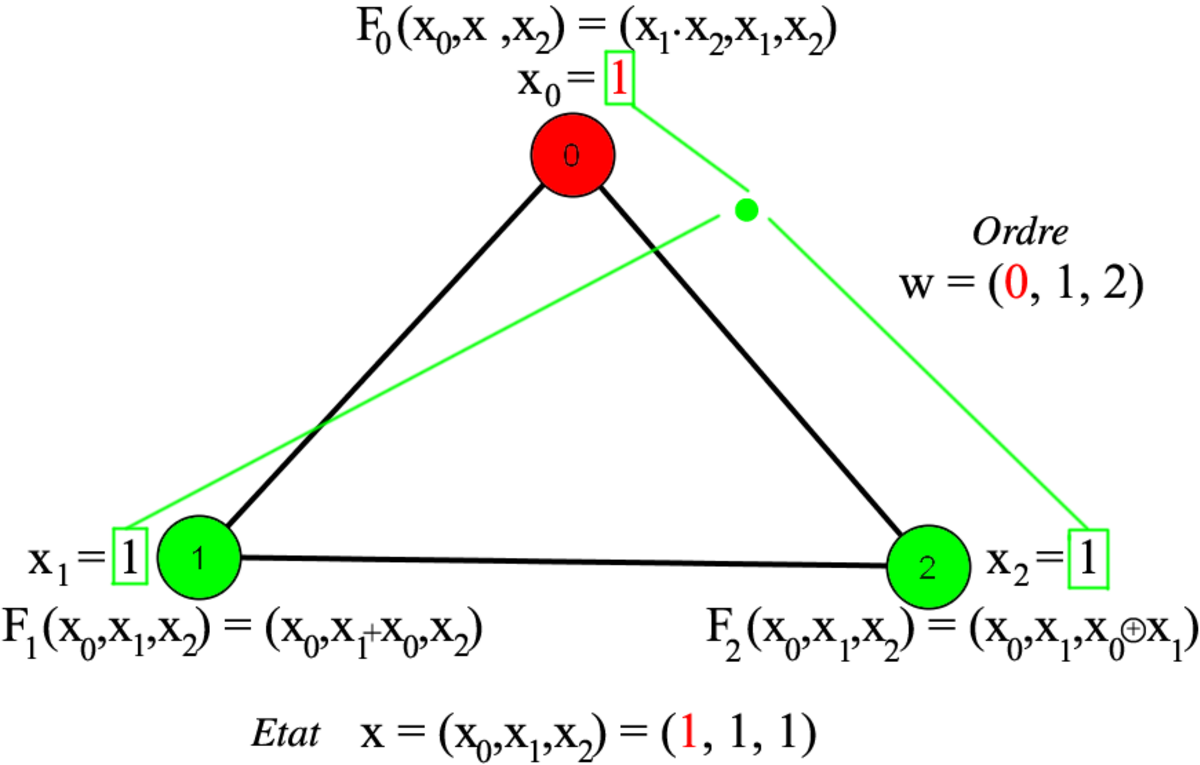
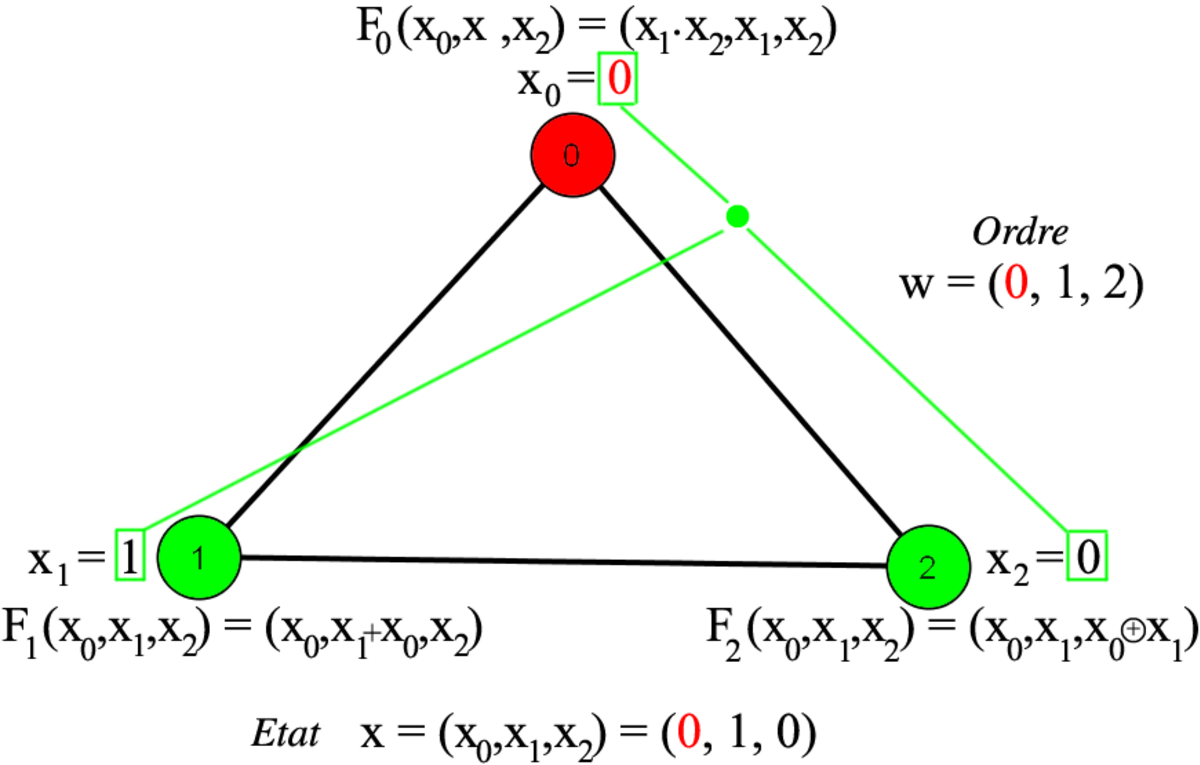
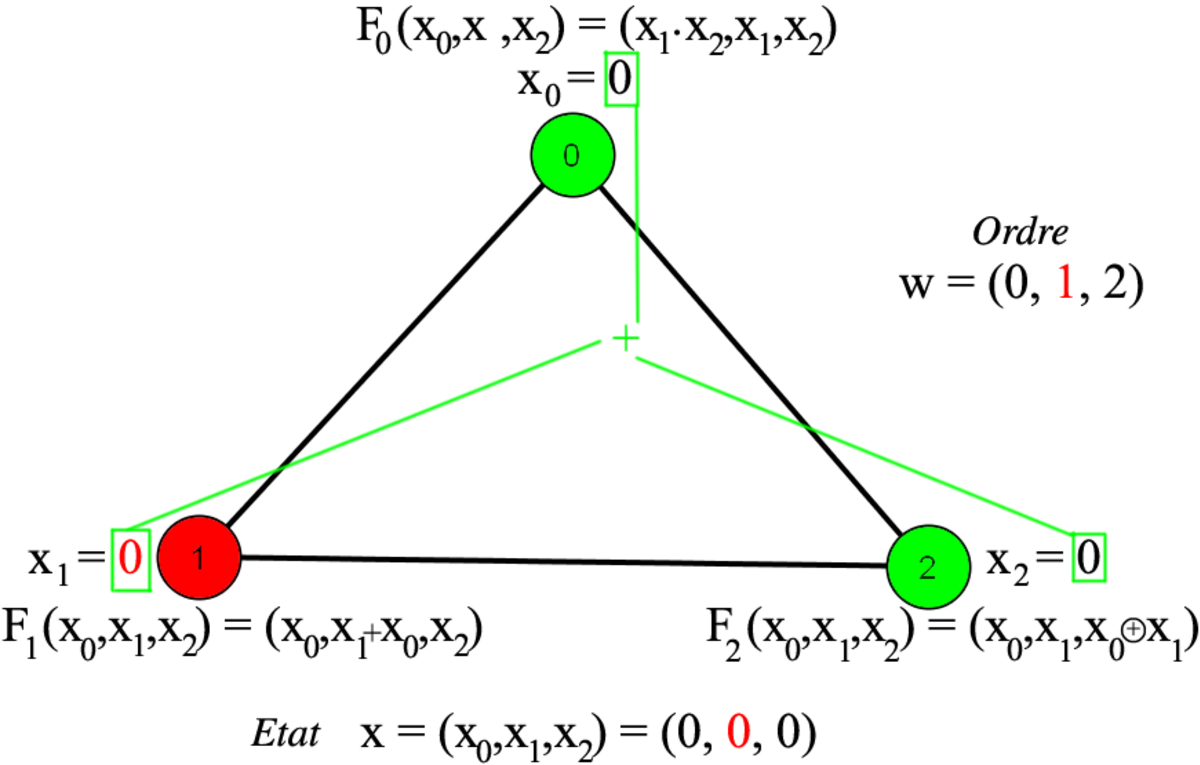
La définition d'un système dynamique séquentiel peut se faire en définissant successivement les éléments suivants : le graphe G (quels sont les sommets et les arêtes), les états possibles K des sommets, les fonctions mettant à jour les états, et l'ordre de mise à jour. Dans cet exemple, le graphe est formé de 3 sommets numérotés 0, 1 et 2, liés en un cycle. L'état xv de chacun des sommets v est 0 ou 1, c'est-à-dire que K = {0,1}. Un graphe où chaque sommet peut prendre deux états est appelé réseau booléen. L'état de l'ensemble du système dynamique est donné par l'état de chacun des trois sommets, soit x = (x0,x1,x2).
Pour mettre à jour les états des sommets, il existe trois fonctions
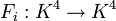
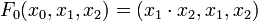

F1(x0,x1,x2) = (x0,x0 + x2,x2), où + représente la fonction OU
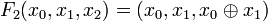
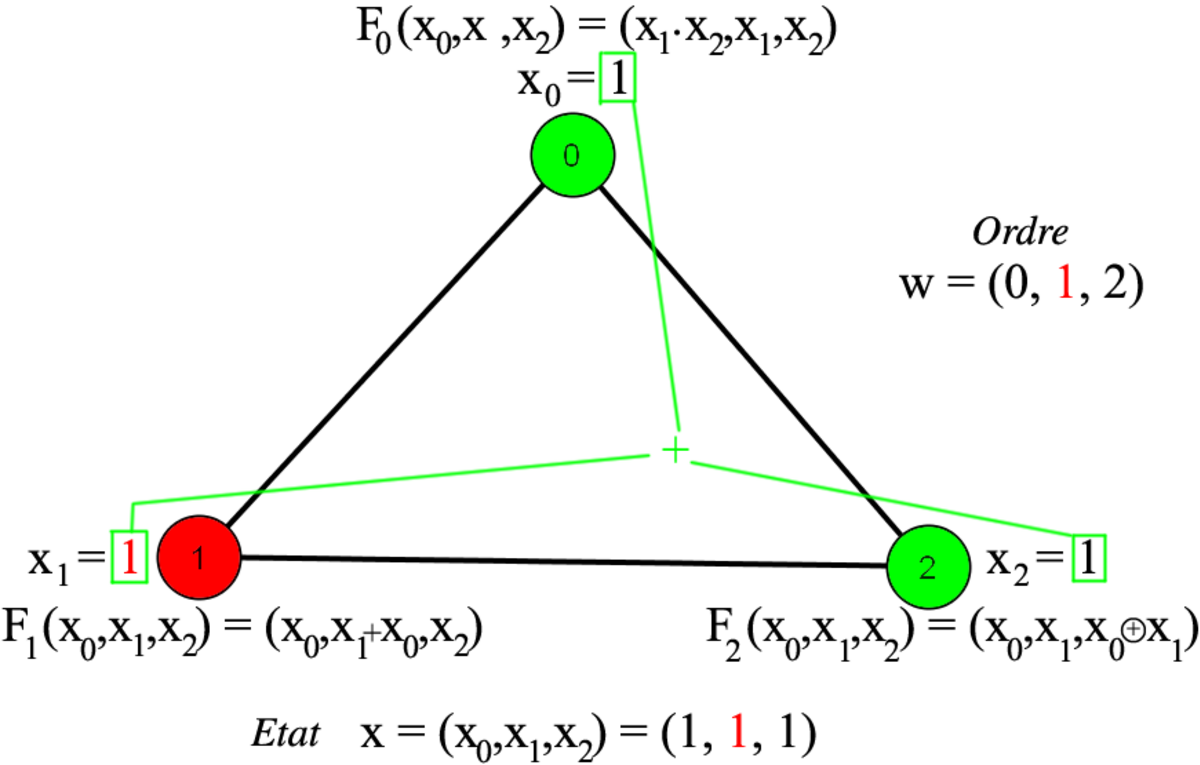
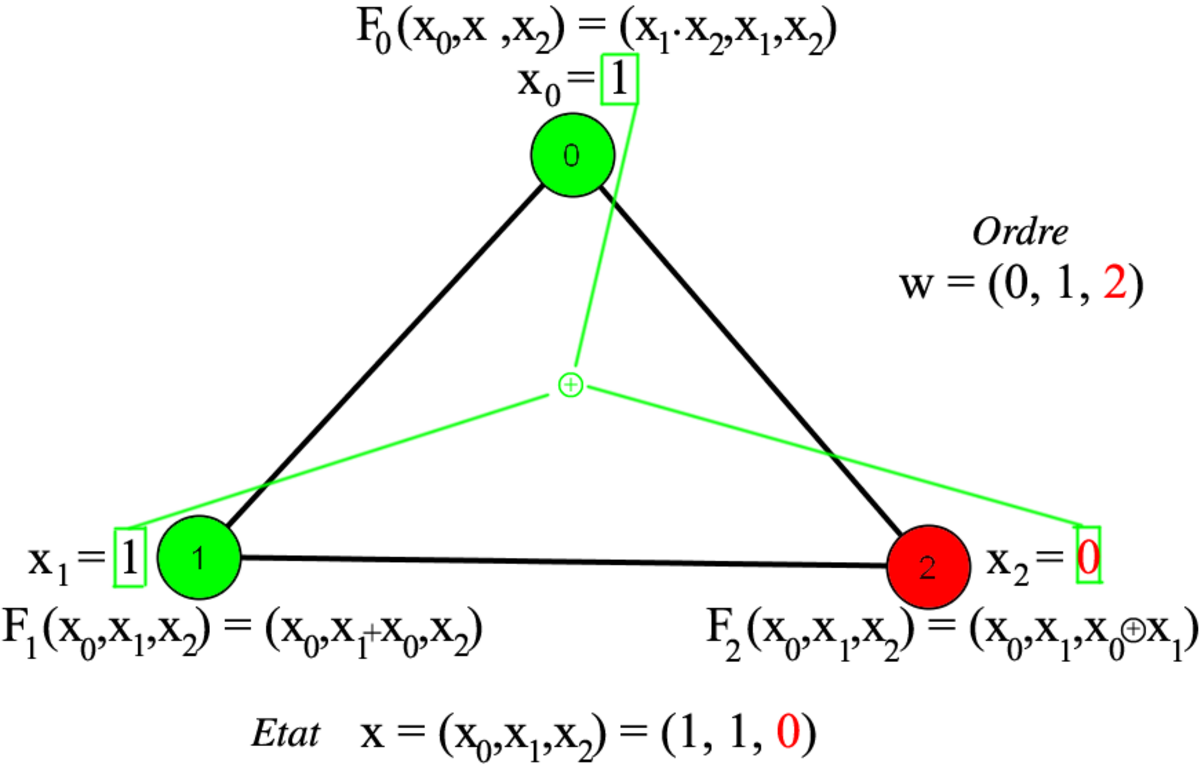
Un ordre possible de mise à jour consiste à exécuter tout d'abord F0, puis F1 et enfin F2. Cet ordre est dénoté w = (0,1,2), et est illustré ci-contre, partant de l'état x = (0,1,1). La notation [FG,(0,1,1)] consiste à appliquer les fonctions dans l'ordre donné par w et à renvoyer le résultat une fois toutes les fonctions appliquées. Ainsi qu'illustré étape par étape, le résultat est [FG,(0,1,1)] = (1,1,0). Formellement, appliquer la troisième fonction sur le résultat de la seconde, elle même venant du résultat de la première, s'écrit
![[F_G,(w_0,w_1,w_2)] = F_{w_2,G} \circ F_{w_1,G} \circ F_{w_0,G}](https://static.techno-science.net/illustration/Definitions/autres/d/d717b9eae2e72fe461572f42baa7e0a4_bcfbd76af15931bc8708b50e138e6a26.png)