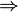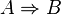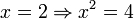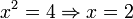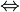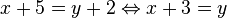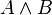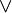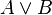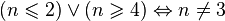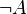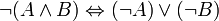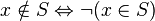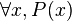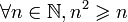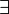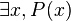Table des symboles mathématiques - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Logique - Autres symboles mathématiques - Autres branches

Introduction

En mathématiques, certains symboles sont fréquemment utilisés. Le tableau suivant représente une aide pour les non-mathématiciens qui ne sont pas habitués à ces symboles. Dans la table, sont précisés pour chaque symbole, le nom, la prononciation et la branche des mathématiques dans laquelle le symbole est principalement utilisé. En plus, la quatrième colonne contient une définition informelle et la dernière donne un court exemple apportant une explication sur l'utilisation du symbole.

Du fait de leur utilisation répandue, il existe un grand nombre de façons différentes de représenter certains symboles. Ce tableau ne saurait prétendre à l'exhaustivité.

Symbole (TeX)	Symbole (utf8)	Nom	Signification	Exemples
		Prononciation
		Branche
$\Rightarrow\,$	⇒	Implication	$A \Rightarrow B\,$ signifie « si A est vraie, alors B est vraie aussi ; si A est fausse alors on ne peut rien dire de la vérité de B ». Parfois, on utilise $\rightarrow\,$ au lieu de $\Rightarrow\,$	$x = 2 \Rightarrow x^2 = 4\,$ est vraie, mais $x^2 = 4 \Rightarrow x = 2\,$ est fausse (puisque x=−2 est aussi une solution).
		« implique » ou « si... alors »
		Logique
$\Leftrightarrow$	⇔	Équivalence logique	$A \Leftrightarrow B$ signifie : « A est vraie quand B est vraie et A est fausse quand B est fausse ».	$x + 5 = y + 2 \Leftrightarrow x + 3 = y\,$
		« si et seulement si » ou « équivaut à »
		Logique
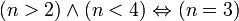$\wedge$	∧	Conjonction logique	$A \wedge B$ est vraie si et seulement si A et B sont vraies (donc fausse si A ou B ou A et B sont fausses)	$(n>2)\wedge (n<4)\Leftrightarrow (n=3)$ , si n est un entier naturel
		« et »
		Logique
$\vee$	∨	Disjonction logique	$A\vee B$ est vraie quand A ou B (ou les deux) sont vraies et fausse quand les deux sont fausses.	$(n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\ne 3$ , si n est un entier naturel
		« ou »
		Logique
$\neg$	¬	Négation logique	$\neg A$ est vraie quand A est fausse et fausse quand A est vraie	$\neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)$ $x\notin S\Leftrightarrow \neg(x\in S)$
		« non »
		Logique
$\forall$	∀	Quantificateur universel	$\forall x, P(x)$ signifie : « P(x) est vraie pour tout x ».	$\forall n\in \mathbb N, n^2\geqslant n$
		« Quel que soit », « pour tout »
		Logique
$\exists$	∃	Quantificateur existentiel	$\exists x, P(x)$ signifie : « il existe au moins un x tel que P(x) soit vraie »	$\exists n\in \N, n+5=2\times n$ (5 répond en effet à la question)
		« il existe au moins un ... tel que »
		Logique

Plage	Nom officiel du bloc
`2000 – 206F`	Ponctuation générale
`2070 – 209F`	Exposants et indices
`20D0 – 20FF`	Signes combinatoires pour symboles
`2150 – 218F`	Formes numérales
`2190 – 21FF`	Flèches
`2200 – 22FF`	Opérateurs mathématiques
`2300 – 23FF`	Signes techniques divers (`2336 – 237A` = symboles APL)
`25A0 – 25FF`	Formes géométriques
`2600 – 26FF`	Symboles divers
`2700 – 27BF`	Casseau
`27C0 – 27EF`	Divers symboles mathématiques - A
`27F0 – 27FF`	Supplément A de flèches
`2900 – 297F`	Supplément B de flèches
`2980 – 29FF`	Divers symboles mathématiques-B
`2A00 – 2AFF`	Opérateurs mathématiques supplémentaires
`2B00 – 2BFF`	Divers symboles et flèches
`3000 – 303F`	Symboles et ponctuation Chinois, japonais et coréen (CJC)
`10100 – 1013F`	Nombres égéens
`1D400 – 1D7FF`	Symboles mathématiques alphanumériques