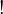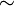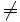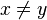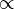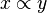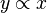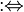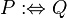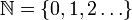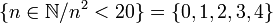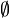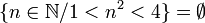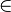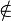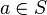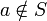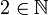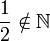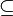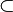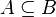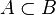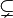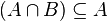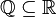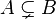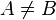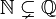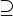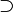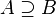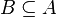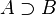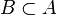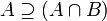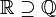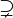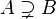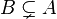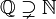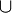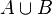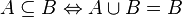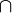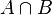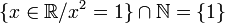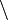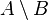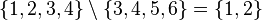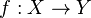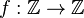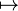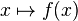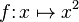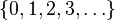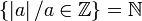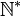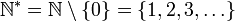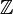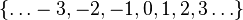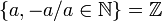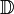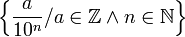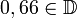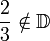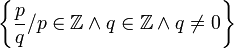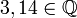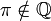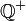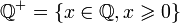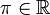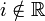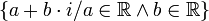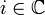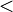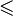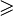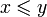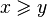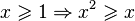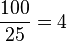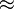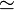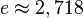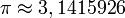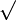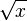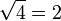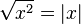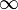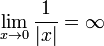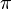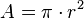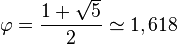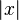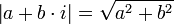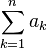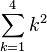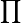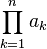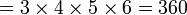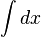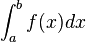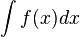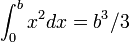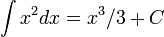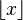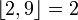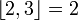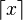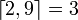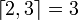Table des symboles mathématiques - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Logique - Autres symboles mathématiques - Autres branches

Autres branches

Symbole (TeX)	Symbole (utf8)	Nom	Signification	Exemples
		Prononciation
		Branche
$! \!\,$	!	Factorielle	n! est le produit : 1 × 2 × ... × n.	6! = 1 × 2 × 3 × 4 × 5 × 6 = 720
		Factorielle (de) n.
		Combinatoire
$\sim$	~	Relation d'équivalence
		« ... est équivalent à ... »
		Théorie des ensembles
		Équivalence	a_n ~ b_n signifie que les suites a_n et b_n sont équivalentes	sin(1/n) ~ 1/n (lorsque n tend vers l'infini)
		« ... est équivalent à ... »
		Analyse
		Distribution de probabilité	X ~ D, signifie : « la variable aléatoire X a la distribution de probabilité D »	X ~ N(0,1), la distribution ou loi normale
		« ... a la distribution de probabilité ... »
		Statistiques
$=\,$	=	Égalité	$x = y$ signifie : « x et y désignent le même objet mathématique »	1 + 2 = 6 − 3
		« est égal à »
		toute branche
$\not=$	≠	Non-égalité	$x\not=y$ signifie : « x et y ne désignent pas le même objet mathématique »	2 ≠ 3
		« n'est pas égal à », « est différent de »
		toute branche
$\equiv$	≡	Congruence
		« identique à », « congru à »
		Arithmétique modulaire
$\propto$	∝	Proportionnalité	$x \propto y$ signifie : « x est proportionnel à y »	si y=2x, alors $y \propto x$
		« est proportionnel à »
		toute branche
$: =$ $:\Leftrightarrow$	:= :⇔	Définition	$x : = y$ signifie : « x est défini comme étant un autre nom de y » $P :\Leftrightarrow Q$ signifie : « P est définie comme étant logiquement équivalente à Q »	$\cosh (x) := {1\over 2}\left(e^x+e^{-x}\right)$ (cosinus hyperbolique) $A \oplus B :\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)$ (OU exclusif)
		« est défini comme »
		le second est très peu utilisé
${,}$	{ , }	Ensemble en extension	${a, b, c}$ désigne l'ensemble dont les éléments sont a, b et c	$\mathbb N = \{0,1,2\ldots \}$ (ensemble des entiers naturels)
		« L'ensemble des ... »
		Théorie des ensembles
${ / }$ ${;}$ ${}$	{ / } { ; } { }	Construction d'ensemble en compréhension	${x / P (x)}$ désigne l'ensemble de tous les x qui vérifient P(x). ${x / P (x)}$ est le même ensemble que ${x; P (x)}$ ou encore que ${x P (x)}$	$\{n\in \mathbb N / n^2<20\} = \{0, 1, 2, 3, 4\}$
		« L'ensemble de tous les ... qui vérifient ... »
		Théorie des ensembles
$\emptyset$ ${}$	∅ {}	Ensemble vide	${}$ et $\emptyset$ désignent l'ensemble vide, l'ensemble qui n'a pas d'élément	$\{n\in \mathbb N / 1<n^2<4\} = \emptyset$
		« Ensemble vide »
		Théorie des ensembles
$\in$ $\notin$	∈ ∉	Appartenance (ou non) à un ensemble	$a\in S$ signifie : « a est un élément de l'ensemble S » $a\notin S$ signifie : « a n'est pas élément de S »	$2\in \mathbb N$ ${1\over 2}\notin \mathbb N$
		« appartient à », « est élément de », « est dans ». « n'appartient pas », « n'est pas élément de », « n'est pas dans »
		Théorie des ensembles
$\subseteq$ $\subset$	⊆ ⊂	Sous-ensemble	$A\subseteq B$ signifie : « tout élément de A est aussi un élément de B » $A\subset B$ a généralement la même signification que $A\subseteq B$ . Signalons toutefois que pour certains, les canadiens français notamment, le symbole $\subset$ représente l'inclusion stricte $\subsetneq$ .	$(A\cap B) \subseteq A$ $\mathbb Q\subseteq \mathbb R$
		« est un sous-ensemble (une partie) de ... », « est inclus dans... »
		Théorie des ensembles
$\subsetneq$	⊈	Sous-ensemble strict, partie stricte	$A\subsetneq B$ signifie $A\subseteq B$ et $A\ne B$ (ou $A\subset B$ et $A\ne B$ quand $\subset$ représente l'inclusion au sens large).	$\mathbb N\subsetneq \mathbb Q$
		« est un sous-ensemble strict de ... », « est strictement inclus dans... »
		Théorie des ensembles
$\supseteq$ $\supset$	⊇ ⊃	Sur-ensemble	$A\supseteq B$ est une autre façon d'écrire $B\subseteq A$ . $A\supset B$ est une autre façon d'écrire $B\subset A$	$A \supseteq (A\cap B)$ $\mathbb R \supseteq \mathbb Q$
		« est un sur-ensemble de ... », « contient... »
		Théorie des ensembles
$\supsetneq$	⊋	Sur-ensemble strict	$A\supsetneq B$ a le même sens que $B\subsetneq A$ .	$\mathbb Q \supsetneq \mathbb N$
		« est un sur-ensemble strict de ... », « contient strictement... »
		Théorie des ensembles
$\cup$	∪	Réunion	$A\cup B$ désigne l'ensemble qui contient tous les éléments de A et de B et seulement ceux-là	$A\subseteq B\Leftrightarrow A\cup B=B$
		« Réunion de ... et de ... », « ... union ... »
		Théorie des ensembles
$\cap$	⋂	Intersection	$A\cap B$ désigne l'ensemble des éléments qui appartiennent à la fois à A et à B, c'est-à-dire les éléments qu'ont les ensembles A et B en commun	$\{x\in \R / x^2=1\}\cap \mathbb N = \{1\}$
		« Intersection de ... et de ... », « ... inter ... »
		Théorie des ensembles
$\setminus$	\	Différence	$A\setminus B$ désigne l'ensemble de tous les éléments de A qui n'appartiennent pas à B	$\{1,2,3,4\}\setminus \{3,4,5,6\} = \{1,2\}$
		« différence de ... et ... », « ... moins ... », « ... privé de ... »
		Théorie des ensembles
$()$ $[]$ ${}$	( ) [ ] { }	Fonction application ; regroupement	f(x) désigne l'image de l'élément x par la fonction f Regroupement: les opérations placées à l'intérieur sont effectuées en premier	Si f est définie par $f (x) = x 2$ , alors f(3) = 3² = 9 (8/4)/2 = 2/2 = 1, mais 8/(4/2) = 8/2 = 4
		« de »
		toute branche
$\to$	→	Fonction	$f:X\to Y$ signifie que la fonction va de X dans Y, ou a pour ensemble de définition X et pour ensemble d'arrivée Y, ou a pour origine X et pour but Y.	Considérons la fonction $f:\mathbb Z\to \mathbb Z$ définie par $f (x) = x 2$
		« de ... vers », « de ... dans », « de ... sur ... »
		toute branche
$\mapsto$	↦	Fonction	$x \mapsto f(x)$ signifie que la variable x a pour image $f (x)$	Au lieu d'écrire que f est définie par f(x) = x², nous pouvons écrire " Soit la fonction $f\colon x \mapsto x^2$ "
		« est envoyé sur », « a pour image »
		toute branche
$\mathbb N$	ℕ	Ensemble des entiers naturels	$\mathbb N$ représente $\{0, 1, 2, 3, \ldots \}$	$\{\left\|a\right\| / a\in \mathbb Z\}=\mathbb N$
		« N »
		Nombre
$\mathbb N ^{*}$	ℕ^*	« N privé de zéro »	$\mathbb N ^{*} = \mathbb N \setminus \{ 0 \} = \{1, 2, 3, \ldots \}$
$\mathbb Z$	ℤ	Ensemble des entiers relatifs	$\mathbb Z$ représente $\{\ldots -3, -2, -1, 0, 1, 2, 3 \ldots \}$	$\{a, -a / a \in \mathbb N\}=\mathbb Z$
		« Z »
		Nombre
$\mathbb D$	ID	Ensemble des nombres décimaux	$\mathbb D$ représente $\left\{{a \over 10^n} / a\in \mathbb Z \wedge n\in \mathbb N\right\}$	$0,66 \in \mathbb D$ ${2 \over 3} \notin \mathbb D$
		« D »
		Nombre
$\mathbb Q$	ℚ	Ensemble des nombres rationnels	$\mathbb Q$ représente $\left\{{p\over q} / p\in \mathbb Z \wedge q\in \mathbb Z\wedge q\ne 0\right\}$	$3,14\in \mathbb Q$ $\pi \notin \mathbb Q$
		« Q »
		Nombre
$\mathbb Q ^{+}$	ℚ⁺		$\mathbb Q ^{+} = \{ x \in \mathbb Q, x \geqslant 0 \}$
$\R$	ℝ	Ensemble des nombres réels	$\R$ représente l'ensemble des limites des suites de Cauchy de $\mathbb Q$	$\pi \in \R$ $i \notin \R$ (i étant le nombre complexe tel que $i 2 = - 1$ )
		« R »
		Nombre
$\mathbb C$	ℂ	Ensemble des nombres complexes	$\mathbb C$ représente $\{a+b\cdot i / a\in \R \wedge b\in \R\}$	$i\in \mathbb C$
		« C »
		Nombre
$<\,$ $>\,$	< >	Comparaison	$x < y$ signifie que x est strictement inférieur à y (ou x est inférieur à y). $x > y$ signifie que x est strictement supérieur à y (ou x est supérieur à y).	$x<y\Leftrightarrow y>x$
		« est strictement inférieur à », « est strictement supérieur à »
		Relation d'ordre
$\leqslant$ $\geqslant$	≤ ou ⩽ ≥ ou ⩾	Comparaison	$x\leqslant y$ signifie que x est inférieur ou égal à y. $x\geqslant y$ signifie que x est supérieur ou égal à y.	$x\geqslant 1\Rightarrow x^2\geqslant x$
		« est inférieur ou égal à » ; « est supérieur ou égal à »
		Relation d'ordre
$+\,$	+	Addition	4 + 6 = 10 signifie que si quatre est ajouté à six, alors la somme ou le résultat est égal à dix.	43 + 65 = 108 2 + 7 = 9
		« plus »
		Arithmétique
$-\,$	-	Soustraction	9 - 4 = 5 signifie que si quatre est ôté (retranché) de neuf, alors le résultat est égal à 5. Le signe moins peut aussi être placé immédiatement à gauche d'un nombre pour le rendre négatif. Par exemple, 5 + (-3) = 2 signifie que si cinq et le nombre négatif moins trois, sont ajoutés, alors le résultat est égal à deux.	87 - 36 = 51
		« moins »
		Arithmétique
$\times$	×	Multiplication	3 × 2 = 6 signifie que si trois est multiplié par deux, alors le produit est égal à six.	23 × 11 = 253
		« fois »
		Arithmétique
$\cdot /\cdot$	÷	Division	8 ÷ 4 = 2 signifie que huit divisé par quatre est égal à deux.	100 ÷ 4 = 25
		« divisé par »
		Arithmétique
${\cdot \over \cdot}$	/	fraction	${9 \over 4}$ représente la fraction neuf quarts. / peut être aussi utilisé pour représenter la division.	${100 \over 25} = 4$
		« sur »
		Arithmétique Nombre
$\approx$ et $\simeq$	≈ ou ≃	Approximation	$e\approx 2,718$ à 10^-3 près signifie qu'une valeur approchée de e à 10^-3 près est 2,718.	$\pi \approx 3,1415926$ à 10^-7 près.
		« approximativement égal à »
		Nombre réel
$\sqrt{ }$	√	Racine carrée	$\sqrt x$ représente le nombre réel positif dont le carré est égal à x.	$\sqrt 4=2$ $\sqrt {x^2}= \left\|x\right\|$
		« Racine carrée de ... »
		Nombre
$\infty$	∞	Infini	$+\infty$ et $-\infty$ sont des éléments de la droite réelle achevée. $\infty$ apparaît dans les calculs de limites. $\infty$ est un point adjoint au plan complexe pour le rendre isomorphe à une sphère (sphère de Riemann)	$\lim_{x\to 0} {1\over \|x\|}= \infty$
		« Infini »
		Nombre
$\pi\,$	π	π	π est le rapport de la circonférence d'un cercle à son diamètre.	$A=\pi \cdot r^2$ est l'aire d'un disque de rayon r
		« Pi »
		Géométrie euclidienne
$\varphi$	ϕ ou φ	« nombre d'or »		$\varphi = \frac{1 + \sqrt{5}}{2} \simeq 1,618$
$e$	e	« e »	e est la base des logarithmes naturels.	exp(1) = e ≈ 2,718
$\left\|\cdot \right\|$	\| \|	Valeur absolue ou module d'un nombre complexe ou cardinal d'un ensemble	$\left\|x\right\|$ désigne la valeur absolue de x (ou le module de x). $\| A \|$ désigne le cardinal de l'ensemble A et représente, lorsque A est fini, le nombre d'éléments de A.	$\left\|a+b\cdot i\right\|=\sqrt {a^2+b^2}$
		« Valeur absolue de... », « module de ... » ; « cardinal de ... »
		Nombre ou Théorie des ensembles
$\sum$	∑	Somme	$\sum_{k=1}^n a_k$ se lit « somme de a_k pour k de 1 à n », et représente a₁ + a₂ + ... + a_n	$\sum_{k=1}^4 k^2$ $= 1 2 + 2 2 + 3 2 + 4 2$ $= 30$
		« Somme de ... pour ... de ... à ... »
		Arithmétique
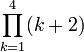
$\prod$	∏	Produit	$\prod_{k=1}^n a_k$ se lit « produit de a_k pour k de 1 à n », et représente : a₁·a₂·...·a_n	$\prod_{k=1}^4 (k+2)$ $=3\times 4\times 5\times 6=360$
		« Produit de .. pour .. de .. à .. »
		Arithmétique
$\int dx$	∫,∬,∭,∮,∯ ou ∰	Intégrale	$\int_a^b f(x) dx$ se lit « Intégrale de a à b de f de x dx », et représente l'aire algébrique du domaine délimité par la courbe représentative de f, l'axe des abscisses et les droites d'équation x = a et x = b $\int f(x) dx$ se lit « intégrale de f de x dx, et représente une primitive de f	$\int_0^b x^2 dx = b^3/3$ $\int x^2 dx = x^3/3+C$ (C désignant une constante)
		« Intégrale (de .. à ..) de .. d-.. »
		Analyse
$\left\lfloor x \right\rfloor$	$\left\lfloor \right\rfloor$	Partie entière	$\left\lfloor x \right\rfloor$ se lit « Partie entière de x», et représente la partie entière inférieure de x	$\left\lfloor 2,9 \right\rfloor = 2$ $\left\lfloor 2,3 \right\rfloor = 2$
		« Partie entière de .. »
		Nombre
$\left\lceil x \right\rceil$	$\left\lceil \right\rceil$	Partie entière par excès	$\left\lceil x \right\rceil$ se lit « Partie entière par excès de x », et représente l'entier supérieur à x	$\left\lceil 2,9 \right\rceil = 3$ $\left\lceil 2,3 \right\rceil = 3$
		« Partie entière par excès de .. »
		Nombre

Autres symboles mathématiques

- Introduction - Logique - Autres symboles mathématiques - Autres branches

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.209 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise