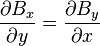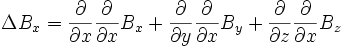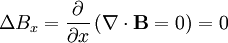Théorème d'Earnshaw - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique, en électromagnétisme classique, le théorème d'Earnshaw établit qu'un ensemble de charges ponctuelles ne peut être maintenu dans un équilibre stable uniquement par des interactions d'ordre électrostatique entre les charges.
Le théorème fut prouvé pour la première fois en 1842 par Samuel Earnshaw. On l'utilise couramment pour les champs magnétiques, mais il fut à l'origine étudié pour les cas électrostatiques. Il s'applique en réalité à toute combinaison de forces qui suivent une loi en

Explications
Ce théorème est une conséquence du théorème de Gauss. Intuitivement, si on considère une particule en équilibre stable, de petites perturbations ne devraient pas briser cet équilibre : elle devrait revenir à sa position précédente. Cela découle du fait que toutes les lignes de champ du champ de forces autour de ce point se dirigent vers cette position d'équilibre.
Ainsi, la divergence du champ à proximité de la position d'équilibre est négative strictement si le champ n'est pas identiquement nul. Le théorème de Gauss prétend cependant qu'une telle chose est impossible : la force F(r) qui s'exerce sur la particule, qui dérive d'un potentiel satisfaisant l'équation de Laplace, doit être de divergence nulle :
dans le vide.
Ainsi, les lignes de champ ne convergent vers aucun point de l'espace vide, un équilibre stable ne peut donc y exister. On dit aussi qu'il n'y a pas de minima ni de maxima locaux du potentiel.
Le théorème établit par ailleurs qu'il n'existe aucune configuration statique d'aimants qui permettrait la lévitation stable d'un objet contre la gravité, même si les forces magnétiques surpassent de beaucoup la force d'attraction gravitationnelle. La lévitation magnétique est cependant possible, si on peut faire varier le champ magnétique dans le temps.
Le théorème d'Earnshaw, en parallèle avec l'instabilité des particules dans le modèle de Bohr de l'atome, à cause de la radiation, suggéra une explication quantique de la structure atomique.
Démonstration pour des dipôles magnétiques
Introduction
Bien qu'une démonstration dans le cas général puisse être donnée, on considère ici trois cas particuliers.
Le premier est celui d'un dipôle magnétique de moment magnétique dipolaire constant, de direction fixe. Les deux cas suivants sont ceux d'un dipôle d'orientation variable, qui s'aligne dans le sens (respectivement dans le sens inverse) des lignes de champ d'un champ magnétique externe. Dans les matériaux paramagnétiques (respectivement diamagnétiques), les dipôles sont alignés dans le sens (respectivement, dans le sens inverse) des lignes de champ.
Lemmes utiles
Les lemmes établis dans cette section seront utiles à l'étude des cas particuliers suivants.
L'énergie U d'un dipôle magnétique M dans un champ magnétique externe B est
Le dipôle sera stable si et seulement si son énergie atteint un minimum, c’est-à-dire si le laplacien de l'énergie est positif :
Enfin, puisqu'à la fois la divergence et le rotationnel d'un champ magnétique sont nuls en l'absence de courants et de variations du champ électrique, les laplaciens des composantes du champ magnétique sont nuls :
Une démonstration sera donnée à la toute fin de cet article.
Démonstrations
L'énergie du dipôle d'orientation fixe et de moment constant est :
Dans ce cas, le laplacien de l'énergie est toujours nul :
Le dipôle est ainsi privé de minimum (et de maximum) d'énergie : il n'y a aucun point de l'espace stable dans toutes les directions, ou instable dans toutes les directions.
Les dipôles alignés en sens direct ou indirect avec le champ externe correspondent respectivement aux matériaux paramagnétiques et diamagnétiques. L'énergie est alors donnée par :
Où k est une constante positive pour les matériaux paramagnétiques, et négative pour les matériaux diamagnétiques. Alors :
On montre ainsi que les matériaux paramagnétiques possèdent un maximum (mais pas de minimum) d'énergie, et inversement pour les matériaux diamagnétiques.
Enfin, le moment magnétique d'un aimant aligné avec le champ est donné par :
Son énergie est :
Il s'agit justement de la racine carrée de l'énergie du cas paramagnétique (ou diamagnétique) discuté ci-dessus. La fonction racine carrée étant strictement croissante, elle induit une bijection qui conserve les maxima et minima obtenus dans les cas paramagnétiques ou diamagnétiques.
On ne connait cependant aucune configuration stable d'aimants permettant la lévitation : il doit exister d'autres raisons qui s'opposent au maintien de dipôles anti-alignés avec un champ (sans mouvement rotatoire, voir Levitron vidéo).
Dipôle de direction fixe
Nous allons montrer qu'en tout point de l'espace :
L'énergie U du dipôle M soumis à un champ externe est encore :
Le laplacien de l'énergie est alors :
En développant, puis en réduisant les termes du laplacien, si M est une constante, on obtient :
soit
mais les laplaciens des composantes du champ magnétique sont nuls dans le vide (en l'absence de radiations). La démonstration s'achève donc en obtenant :
Dipôle aligné dans un champ externe
Le cas d'un dipôle paramagnétique (ou diamagnétique) est considéré tout d'abord. Son énergie est donnée par :
En développant puis en réduisant son expression, on obtient :
mais puisque le laplacien de chaque composante est nul dans le vide :
Enfin, puisque le carré d'un nombre réel est positif, on obtient :
Laplacien du champ magnétique
On montre dans cette section de le laplacien de chaque composante du champ magnétique est nul. Nous aurons besoin de faire appel aux propriétés des champs magnétiques, tels que la divergence nulle et le rotationnel nul en l'absence de courant et de radiations, qui découlent des équations de Maxwell.
Le laplacien de la composante selon x du champ magnétique est :
Le rotationnel de B étant nul,
et
On a donc :
Or, Bx est différentiable (et on fait l'hypothèse qu'il le soit infiniment). Alors :
La divergence de B est nulle, donc constante :
Il en est de même pour les composantes selon y et z du champ magnétique.








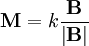
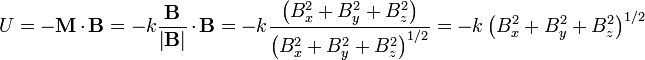


![\Delta U = -\left[ \frac{\partial^2 (M_x B_x + M_y B_y + M_z B_z)}{\partial x^2} + \frac{\partial^2 (M_x B_x + M_y B_y + M_z B_z)}{\partial y^2} + \frac{\partial^2 (M_x B_x + M_y B_y + M_z B_z)}{\partial z^2} \right]](https://static.techno-science.net/illustration/Definitions/autres/3/3a2873c6f41b3faeb7c6d5164a5b56b2_9abfbe7f684dadce6c772e015bab5c6f.png)
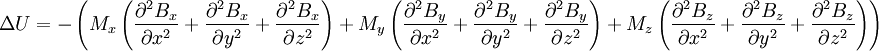



![\Delta \left( B_x^2 + B_y^2 + B_z^2 \right) = 2 \left[ \left| \nabla B_x \right|^2 + \left| \nabla B_y \right|^2 + \left| \nabla B_z \right|^2 + B_x \nabla^2 B_x + B_y \nabla^2 B_y + B_z \nabla^2 B_z \right]](https://static.techno-science.net/illustration/Definitions/autres/1/16d0ce2005c227bd26991e2841fe35eb_a0f42973319cc21cb28b6e3839f5af69.png)
![\Delta \left( B_x^2 + B_y^2 + B_z^2 \right) = 2 \left[ \left| \nabla B_x \right|^2 + \left| \nabla B_y \right|^2 + \left| \nabla B_z \right|^2 \right]](https://static.techno-science.net/illustration/Definitions/autres/6/67680390104bb2e2a54407d244727046_f447f08122457a13289472fcdb8ca676.png)