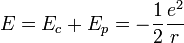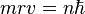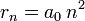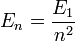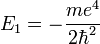Modèle de Bohr - Définition

Introduction

Le modèle de Bohr est une théorie physique, basée sur le modèle planétaire de Rutherford, cherchant à comprendre la constitution d'un atome, et plus particulièrement, celui de l'hydrogène et des ions hydrogénoïdes (ions ne possédant qu'un seul électron).

Principe

Schématisation des orbites circulaires dans le modèle de Bohr.

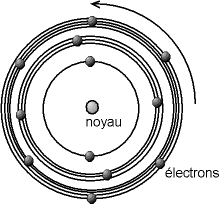
Ce modèle est un complément du modèle planétaire d'Ernest Rutherford qui décrit l'atome d'hydrogène comme un noyau massif et chargé positivement, autour duquel se déplace un électron chargé négativement.

Le problème posé par ce modèle est que l'électron, charge électrique accélérée, devrait selon la physique classique, rayonner de l'énergie et donc finir par s'écraser sur le noyau.

Niels Bohr propose d'ajouter deux contraintes :

1. L'électron ne rayonne aucune énergie lorsqu'il se trouve sur une orbite stable (ou orbite stationnaire). Ces orbites stables sont différenciées, quantifiées. Ce sont les seules orbites sur lesquelles l'électron peut tourner.
2. L'électron ne rayonne ou n'absorbe de l'énergie que lors d'un changement d'orbite.

Pour commodité de lecture, les orbites possibles de l'électron sont représentées dans la littérature comme des cercles de diamètres quantifiés (Dans la réalité, il n'existe pas de position ni de vitesse précise d'un électron, et il ne peut donc parcourir un « cercle » ; son orbitale peut en revanche être parfois sphérique).

Théorie

L'atome d'hydrogène est modélisé par un électron de masse m tournant autour du proton.

L'énergie mécanique

L'interaction entre ces deux particules est électrostatique: la force intervenant est la force de Coulomb. Ceci nous permet donc d'écrire l'énergie potentielle de l'électron à une distance r du noyau :

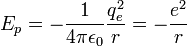
• ε₀ est la permittivité du vide
• q_e est la charge de l'électron
• , par souci de simplification d'écriture ( cf système d'unités atomiques ).

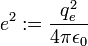
D'autre part, comme il est question d'un mouvement à force centrale, l'accélération de cet électron vaut où v est la vitesse de l'électron, et est le vecteur unitaire centrifuge. Le principe fondamental de la dynamique implique alors :

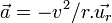
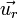
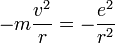
On peut alors calculer l'énergie cinétique :

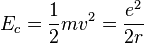
Finalement, on obtient l'énergie mécanique :

Quantification

Ici intervient alors la quantification du moment cinétique  : selon l'hypothèse de Bohr :
où n est un entier positif non nul, et est la constante de Planck "réduite" ( d'un facteur 2 π).
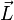
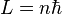
 : seules les orbites ayant ce moment cinétique ne rayonnent pas : les orbites sont donc "quantifiées" par le nombre entier n positif. Cette relation s'écrit :

Cette quantification a été confirmée par l'expérience de Franck et Hertz. L'intérêt de cette expérience est de montrer que la quantification n'est pas seulement due à la quantification de la lumière, mais bien à la quantification de l'orbite des électrons présents dans l'atome.

Résultats

• Les deux équations précédentes:

et

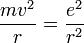
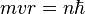
permettent de calculer la distance entre le noyau et l'électron, r ( ainsi que la vitesse v ):

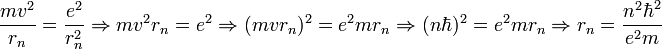
où est le rayon de Bohr, soit environ 53 pm.

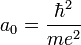
• L'énergie totale de l'électron est aussi quantifiée :

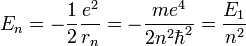
avec

E₁ est une unité d'énergie, appelée énergie de Rydberg (cf constante de Rydberg), et vaut environ -13.6 eV.

Néanmoins cette théorie, même modifiée par Sommerfeld pour tenir compte des orbites elliptiques, ne survivra pas à la révolution de la mécanique quantique en 1926.