Théorème de complétude de Gödel - Définition

L'existence d'un modèle sous l'hypothèse de cohérence

Nous allons prouver le théorème de complétude sous la forme suivante.

Si une formule est cohérente alors elle est satisfaisable. Si , alors .

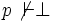
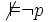
En fait nous prouverons une version renforcée de ce théorème.

Si un ensemble d'axiomes est cohérent alors il est satisfaisable.

Un ensemble d'axiomes est cohérent lorsqu'aucune contradiction n'est prouvable à partir d'un nombre quelconque, fini, de ces axiomes. Il est satisfaisable lorsqu'il y a un modèle dans lequel les axiomes sont tous vrais. Cette version renforcée du théorème est utile en particulier pour énoncer le paradoxe de Skolem, parce qu’elle permet d’appliquer le théorème de complétude à des systèmes infinis d’axiomes.

Commençons par montrer comment remplacer un système d’axiomes du calcul des prédicats par un système équivalent d’axiomes du calcul des propositions. Pour cela, on commence par mettre chaque axiome sous une forme prénexe.

Une formule du calcul des prédicats est toujours équivalente à une formule mise sous forme prénexe, c’est-à-dire une formule dans laquelle tous les quantificateurs universels et existentiels sont placés au début et non à l'intérieur des sous-formules. On peut toujours prouver qu'une formule est équivalente à une formule prénexe avec les règles de déduction suivante :

• de déduire , pourvu que q ne contienne pas x comme variable libre. (Si elle la contient, il suffit de substituer à x dans une autre variable qui n'apparaît pas dans q).
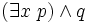
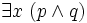
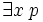
• de déduire , pourvu également que q ne contienne pas x comme variable libre.
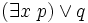
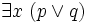
• deux autres règles semblables pour le quantificateur universel .
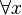
• de déduire .
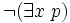
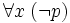
• de déduire .

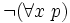
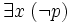
Toutes ces règles sont des règles dérivées dans le système de déduction naturelle et elles font toutes passer d'une prémisse à une conclusion équivalente. Par itération elles fournissent une formule prénexe équivalente à la formule initiale.

De la forme prénexe d'un axiome, on passe à sa forme de Skolem en introduisant de nouveaux opérateurs fondamentaux, autant qu’il en faut pour faire disparaître tous les quantificateurs existentiels dans les axiomes. Par exemple, l’axiome prénexe est remplacé par où − est un nouvel opérateur unaire. Pour un axiome de la forme , on introduit un opérateur binaire, * par exemple, et on prend pour axiome

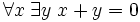
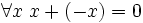
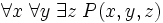
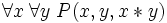
On construit alors un univers, un domaine des êtres nommés. Les noms des objets de base sont ceux qui sont mentionnés dans les axiomes. S’il n’y en a pas, on en introduit un, qu’on peut appeler comme on veut, 0 par exemple.

L’ensemble des noms d’objet est celui obtenu par induction à partir des noms des objets de base et des noms de tous les opérateurs mentionnés dans les axiomes d’origine ou introduits par la méthode ci-dessus exposée. L’univers U est l’ensemble de tous les êtres ainsi nommés.

Chaque forme de Skolem d'un axiome peut être conçue comme un schéma d’axiomes à l'intérieur du calcul des propositions. On supprime tous les quantificateurs universels et on remplace toutes les variables alors libres par des noms d’objet. À chaque axiome de départ on associe ainsi un ensemble infini de formules du calcul des propositions. La réunion de toutes ces formules associées à tous les axiomes de départ, est le nouveau système d’axiomes, non quantifiés, équivalent au système d’origine.

Montrons maintenant que si un sous-ensemble fini du système d'axiomes non-quantifiés est incohérent alors le système d'axiomes d'origine est lui aussi incohérent. Soit C une conjonction incohérente d'axiomes non-quantifiés. Soit C' la formule obtenue à partir de C en remplaçant toutes ses constantes par des variables distinctes, de telle façon que C ne contienne plus d'opérateurs d'objet, et en quantifiant existentiellement sur toutes ces variables. Comme C est incohérente, C' l'est aussi. Mais C' peut être prouvée à partir d'un nombre fini des axiomes d'origine, qui sont donc eux aussi incohérents.

Si un système d'axiomes est cohérent tous les sous-ensembles finis du système d'axiomes non quantifiés sont également cohérents. D'après le théorème de complétude du calcul des propositions, ils sont donc tous satisfaisables. D'après le théorème de compacité, le système - infini - d'axiomes non quantifiés est lui aussi satisfaisable. Comme un modèle du système d'axiomes non-quantifiés est également un modèle du système d'origine, on a prouvé l'existence d'un modèle pour tout système cohérent d'axiomes.