Théorème de complétude de Gödel - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de complétude du calcul des prédicats du premier ordre a été démontré par Kurt Gödel (1929, thèse de doctorat, sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au sens où toute proposition qui est vraie dans ce calcul peut être démontrée.
Diverses formulations équivalentes du théorème de complétude
Le théorème de complétude est un méta-théorème qui relie deux concepts : celui de déduction logique et celui de validité d'un énoncé.
Systèmes de déduction et validité
Le premier concept à définir est donc celui de déduction logique, il dit qu'on peut donner un nombre fini d’axiomes, de schémas d’axiomes ou de règles d'inférence pour décrire ou formaliser la partie purement logique de la déduction, autrement dit toutes les démonstrations qui sont décrites en des étapes élémentaires de raisonnement sont obtenues à partir de ces principes.
La validité logique d’un axiome, d'un schéma d'axiomes ou d'une règle d'inférence est garantie par des modèles. Ainsi, une règle de déduction est valide lorsque tout modèle de ses prémisses est aussi un modèle de sa conclusion. Un axiome logique est valide lorsqu’il est vrai dans tous les modèles. Un schéma d’axiomes est un principe logique valide lorsque tous les axiomes produits par ce schéma sont des axiomes logiques valides. Un système de principes logiques est valide ou correct lorsque ses axiomes, ses schémas d’axiomes et ses règles de déduction sont valides. Une preuve est logiquement valide lorsqu’elle peut être formalisée dans le cadre d’un système logique valide.
Nous allons prouver que la liste des quinze règles de déduction naturelle est un système complet des principes de la logique du premier ordre. Ce théorème est équivalent à celui de Gödel. Mais la preuve de Gödel est basée sur une autre formulation des principes logiques, celle des Principia Mathematica de Whitehead et Russell.
Quelques définitions
Pour cela, donnons quelques définitions :
- celles relatives à l'utilisation de modèles (du premier ordre) : satisfaisabilité et falsifiabilité, loi logique et contradiction logique, conséquence logique, prouvabilité
- Une formule du calcul des prédicats est satisfaisable ou possiblement vraie lorsqu’elle est vraie dans au moins un modèle. Elle est universellement valide, ou est une loi logique, lorsqu’elle est vraie dans tous les modèles. Si p est une loi logique, on note
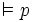
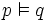
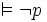
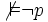
- celles relatives aux systèmes de déduction (pour le calcul des prédicats du premier ordre) : cohérence et incohérence, prouvabilité.
- Si p est une formule du calcul des prédicats, p est prouvable dans un système de déduction pour la logique L, lorsqu’il existe une preuve de p dans L, au sens où les règles de déduction de L suffisent pour déduire p en un nombre fini d'étapes dans L, ce qu'on note
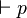
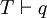
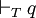

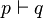
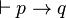
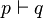
Notons

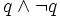
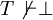
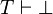
Un système de déduction correct se doit de ne pouvoir prouver, à partir de formules vraies, que des propositions vraies, en particulier, on attend que, si
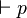
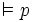
La complétude
Le théorème de complétude se préoccupe de la réciproque de la correction. Cela signifie que le système de déduction L se doit d'être suffisamment complet de façon à être capable de démontrer toute loi logique, c'est-à-dire toute formule vraie dans tout modèle. Le théorème de complétude peut être énoncé sous la forme suivante (exprimée pour une formule, une forme plus forte du théorème de complétude s'écrit pour un nombre éventuellement infini de formules) :
Il existe des systèmes de déduction logiques valides L qui satisfont aux conditions équivalentes suivantes :
- pour toutes formules p et q (du calcul des prédicats du premier ordre), si q est une conséquence logique de p alors q est prouvable à partir de p dans L. Si
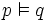
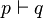
- Pour toute formule p, si p est une loi logique alors p est prouvable. Si
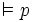
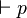
- Pour toute formule p, si p est une contradiction logique alors (non p) est prouvable. Si
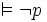
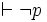
- Pour toute formule p, si p est une contradiction logique alors p est incohérente dans L. Si
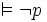
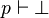
- Pour toute formule p, si p est cohérente dans L alors p est satisfaisable. Si
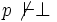
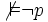
On peut enfin remarquer qu'un ensemble défini par induction avec un nombre fini de principes (axiomes, schémas d'axiomes et règles de déduction) est énumérable. Autrement dit, toutes les théories axiomatiques usuelles sont des ensembles énumérables. Le théorème de complétude dit qu'il existe des théories axiomatiques complètes de la logique du premier ordre.
Il en résulte que l'ensemble des lois logiques est énumérable.
Cela permet de relier ce théorème de complétude à la théorie de l'indécidabilité, parce qu'on peut prouver que l'ensemble des lois logiques est indécidable. Autrement dit, l'ensemble des formules falsifiables n'est pas énumérable, ou, de façon équivalente, l'ensemble des formules satisfaisables n'est pas énumérable (voir également le théorème d'incomplétude et le théorème de Tarski).

















































