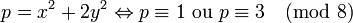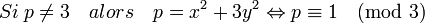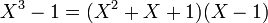Théorème des deux carrés de Fermat - Définition

• 

La démonstration ici est analogue à celle de Dedekind, cependant, l'anneau des entiers est celui d'Eisenstein. Il est composé des nombres complexes de la forme a + b.j où j désigne la racine cubique de l'unité . C'est aussi un anneau euclidien et donc factoriel.

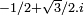
1. Si un nombre premier différent de trois est de la forme x² + 3.y² alors il est congru à un modulo trois.

En effet, le deuxième terme est congru à zéro, modulo trois, un carré est congru à zéro ou à un. En conséquence, si p est différent de trois, comme il est premier, il n'est pas congru à zéro modulo trois il est donc congru à un.

2. Si p est différent de trois et congru à un modulo trois, alors il existe un entier α tel que α² + 3 soit un multiple de p.

Soit le polynôme X³ - 1 dans Z/pZ. Ces racines sont les éléments d'ordre trois dans le groupe (Z/pZ)* qui est un groupe cyclique d'ordre p - 1 (cf Groupe cyclique et anneau). Il en existe trois si et seulement si l'ordre du groupe est un multiple de trois (cf la troisième proposition du Théorème fondamental des groupes cycliques). Le polynôme se factorise de la manière suivante :

Et le polynôme X² + X + 1 admet une racine J dans Z/pZ si, et seulement si, p est congru à un modulo trois. Il suffit alors de remarquer que le carré de 1 + 2.J est égal à -3. Ce qui montre que tout élément α de la classe de 1 + 2.J remplit la condition.

3. Il existe un entier d'Eisenstein de norme égale à p, si p est congru à un modulo trois.

p divise (α + √3.i).(α - √3.i). De plus il ne divise aucun des membres car s'il en divise un, il divise l'autre (c'est son conjugué) et il divise leur différence égale à 2√3.i. Or p ne divise pas 2√3.i, il n'est donc pas irréductible. Et il existe deux entiers d'Eisenstein n et m non unitaires tel que p = n.m et comme la norme de p est égale à p² et qu'une norme est toujours un entier, la norme de n est égale à p. La proposition est démontrée.

4. Il existe deux entiers x et y tel que x² + 3.y² soit égal à p, si p est congru à un modulo trois.

Le point 3. montre l'existence de deux entiers a et b tel que n = a + b.j ait pour norme p. Cependant un entier de la forme a + b.j est de la forme x + y.√3.i si, et seulement si, b est pair. On remarque que la norme de n est égal à a² - a.b + b². a et b ne peuvent être pair en même temps car p serait alors un multiple de quatre, or p est premier. Si a est pair, alors b + a.j possède une norme égale à p et un coefficient pair pour j. Si a et b sont impairs alors a + (a - b).j possède une norme égale à p et un coefficient pair pour j.

• 

Une démonstration est proposée dans l'article Entier quadratique.

Un lemme est utile pour la démonstration de ce théorème:

• Soit p un nombre premier congru à 3 modulo 4. Si une somme de deux carrés d'entiers a² + b² est un multiple de p alors a et b sont des multiples de p.

Si a² + b² est congru à 0 modulo p et si b n'est pas un multiple de p alors a/b est solution de l'équation X² + 1 = 0 dans Z/p Z. Il n'existe pas de telle solution d'après la démonstration du théorème des deux carrés de Fermat. Donc b est un multiple de p et par voie de conséquence a aussi.

• Démonstration du théorème :

Si p est de la forme décrite dans le théorème, alors la puissance de deux s'écrit soit (2^m + 0) si m est paire soit (2^m-1 + 2^m-1) si m est impaire. Les nombres premiers congrus à 1 modulo 4 s'écrivent tous sous forme de somme de deux carrés et les puissances paires de nombres premiers congrus à 3 modulo 4 s'écrivent toutes sous une forme du type (p² + 0)^m. Alors n est produit de sommes de deux carrés et le premier lemme permet de conclure.

Réciproquement supposons que n est somme de deux carrés d'entiers n = a² + b². Soit p un nombre premier congru à 3 modulo 4 élément de la décomposition en facteurs premiers de n. Le deuxième lemme montre que a et b sont des multiples de p. En conséquence a² + b² est un multiple d'un carré de p. Ce qui permet de conclure que toutes les puissances congrues à 3 modulo 4 sont paires.