Théorème des deux carrés de Fermat - Définition

Histoire

Antiquité : premiers résultats

L'intérêt pour les sommes de carrés remonte à l’Antiquité : on trouve de telles sommes dans des tablettes en cunéiforme du début du 2^e millénaire avant notre ère et deux lemmes ajoutés au théorème X. 28 dans les Éléments d'Euclide expliquent comment construire des carrés parfaits sont la somme ou la différence forment encore des carrés parfaits, ou au contraire comment ne pas obtenir un carré en sommant deux carrés.

Mais c’est dans la tradition diophantienne que l’on trouve des traces plus précises sur les nombres sommes de carrés. Les Arithmetica, composées à une date incertaine, contiennent des problèmes dont les solutions cherchées sont rationnelles ou entières. Un grand nombre d’entre eux concerne les nombres carrés ou cubiques (en l’occurrence des carrés ou des cubes de nombres rationnels). À titre d'exemples, le problème 11 du livre II est le suivant : « Ajouter un même nombre à deux nombres donnés de manière que chacun d'eux forme un carré », ou encore le problème 22 du livre IV : « Trouver trois nombres tels que le nombre solide issu de ces nombres [autrement dit, le produit de ces trois nombres], augmenté de chacun d’eux, forme un carré. ». Pour résoudre toutes ces questions, Diophante introduit une « quantité indéterminée d’unités » qu’il appelle « arithme » et exprime en fonction d’elle toutes les données du problème (c’est donc un ancêtre de la notion d’inconnue en algèbre). Il arrive ainsi à trouver une solution numérique particulière, par exemple pour le problème II.11 la solution 97/64 si les nombres donnés sont 2 et 3, et pour le problème IV.22, la solution 1, 34/6 et (2.1/2)/6.

Plusieurs mentions pertinentes pour la détermination des nombres sommes de deux carrés apparaissent de manière dispersée dans divers problèmes. Par exemple, Diophante note sans explication que 15 ne peut être la somme de deux carrés de nombres rationnels au milieu de la solution du problème VI.14. Dans le livre III, il affirme que le nombre 65 est une somme de deux carrés de deux façons différentes, car c'est le produit de 5 et 13, eux-mêmes sommes de deux carrés. Un autre problème concerne le fait de « partager l'unité en deux parties et ajouter à chacun des fragments un nombre donné, de manière à former un carré.  ». Ceci revient à chercher une expression de :

sont des carrés de nombres rationnels. Ici :

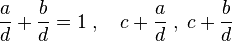
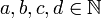
Ceci revient à chercher 2c + 1 comme somme de deux carrés. Diophante dit explicitement que c doit être pair, autrement dit que la division de 2c + 1 par 4 donne pour reste 1.

Certains mathématiciens lecteurs de Diophante étudieront de manière plus systématique et plus arithmétique les nombres sommes de carrés, en particulier la tradition en langue arabe de al-Khazin, al-Sizji, al-Samaw’al, etc.. Leur perspective combine, sur les problèmes diophantiens qui s’y prêtent, des techniques inspirées de l’algèbre naissante et un point de vue euclidien, en particulier une focalisation sur les nombres entiers et des preuves générales. Par exemple, ils montrent qu’une somme impaire de deux carrés premiers entre eux est de la forme 12k+5 ou 12k+1. Un contexte important est l'étude des triangles rectangles en nombres, ou triplets pythagoriciens, c'est-à-dire des nombres vérifiant a² + b² = c² : en effet, si les côtés a, b, c sont premiers entre eux, c lui-même s'écrit comme une somme de carrés.

XVII^e siècle : Les énoncés

C'est en lien direct avec les éditions et commentaires des Arithmétiques de Diophante que l'on trouve au XVII^e siècle une exploration plus sytématique, puis les premiers énoncés complets de ce théorème.

Albert Girard achève ainsi la traduction de Simon Stevin des livres de Diophante et dans ses annotations (publiées en 1634 après sa mort), annonce que les nombres s'exprimant comme somme d'au plus deux carrés sont « les carrés, les nombres premiers de la forme 4k+1, les produits de nombres de ces deux formes et le double de chacun des nombres obtenus », c'est-à-dire un énoncé équivalent à l'énoncé général donné ci-dessus. Aucun élément de preuve n'est cependant apporté.

C'est à peu près à la même date que Marin Mersenne met en place à Paris une académie toute mathématique communiquant les résultats des différents travaux, et appuyée sur un important réseau de correspondants à travers toute l'Europe. Y participent des noms restés plus ou moins célèbres comme Étienne et Blaise Pascal , René Descartes, Bernard Frénicle de Bessy , Gilles Personne de Roberval ou encore Pierre de Carcavi, bibliothécaire du Roi. Cette correspondance est une des deux principales sources pour les travaux arithmétiques de Pierre Fermat, l'autre étant ses propres commentaires à l'édition de Diophante qu'a donnée Claude Gaspard Bachet de Méziriac en 1621. Dans ses travaux de théorie des nombres, Bachet s'inscrit dans la tradition de l'analyse diophantienne entière, il donne de nouveaux exemples numériques en entiers, et surtout des preuves à la mode euclidienne de nombreuses propositions. En particulier il prouve que le produit de deux sommes de deux carrés est une somme de deux carrés, de deux façons différentes ; plus précisément, en notation algébrique actuelle:

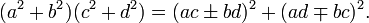
Cette identité est fondamentale pour passer du cas des nombres premiers au cas général.

Mersenne encourage ses correspondants à se proposer mutuellement des problèmes, afin d’en tester la difficulté auprès des autres mathématiciens et de les stimuler dans leurs recherches. L’un des premiers proposés à Fermat en 1636 concerne les sommes de plusieurs carrés, et dès mars 1638, Mersenne indique à Descartes que Fermat a prouvé qu’un nombre de la forme 4’’k’’+3 n’est ni carré, ni somme de deux carrés (rationnels). En 1640, reprenant contact avec Roberval après une interruption de leur correspondance, Fermat lui rappelle ce résultat déjà un peu ancien et explique :

Voici ce que j’ai découvert depuis sur le sujet de la proposition 12 du cinquième Livre de Diophante. Si un nombre donné est divisé par le plus grand carré qui le mesure et que le quotient se trouve mesuré par un nombre premier moindre de l’unité qu’un multiple du quaternaire, le nombre donné n’est ni carré, ni composé de deux carrés (rationnels). ... J’ai démontré ensuite ... [que s]i un nombre est composé de deux carrés premiers entre eux, je dis qu’il ne peut être divisé par aucun nombre premier moindre de l’unité qu’un multiple du quaternaire.

Autrement dit, en termes plus modernes, si on écrit un nombre n sous la forme et qu'un des facteurs premiers p_i est de la forme 4k-1, n n'est pas une somme de carrés, ni en entiers, ni en nombres rationnels (c'est-à-dire ne divise même pas une somme de carrés). Et si p premier divise a² + b², avec a et b premiers entre eux, alors p n'est pas de la forme 4k-1 (c'est donc 2 ou un premier de la forme 4k+1).

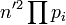
Mais c’est surtout dans une longue missive à Mersenne datée du jour de Noël que Fermat énonce ses fondements pour résoudre tous les problèmes liés aux sommes de carrés. Pour cette raison, le théorème est parfois appelé théorème de Fermat de Noël.

Tout nombre premier [=p], qui surpasse de l’unité un multiple du quaternaire [tel que p = 4k + 1] est une seule fois la somme de deux carrés. De même son carré [p²]. Son cube [p³] et son carré-carré [p⁴] sont chacun deux fois la somme de deux carrés ; son carrécube [p⁵] et son cubecube [p⁶] sont chacun trois fois la somme de deux carrés; etc., à l’infini...

Ce résultat réapparaît dans le contexte de différents problèmes, Fermat y ajoute bientôt le problème de la construction même des carrés. Le théorème sur les sommes de carrés figure aussi dans les fameuses observations que Fermat a écrit en marge de l'édition de Bachet des Arithmétiques de Diophante, observations qu'on connaît par la version posthume publiée par son fils en 1670.

L'interlocuteur le plus important de Fermat sur la théorie des nombres, Frenicle, manifeste d'ailleurs qu'il a trouvé aussi cet énoncé : il demande par exemple à Fermat de trouver le plus petit nombre qui soit somme de deux carrés exactement un nombre de fois donné, et consacre le 5^e exemple de son propre traité La Méthode des Exclusions au problème : « un nombre étant donné, déterminer combien de fois il est la somme de deux carrés ».

Le XVII^e siècle : qu'en est-il des preuves ?

Si l'énoncé est un bien collectif pour ces mathématiciens, il n'en est pas de même de la démonstration. Éliminer les diviseurs premiers de la forme 4k-1 peut se faire en considérant simplement les restes de la division des carrés par 4 : sollicité par Mersenne, comme indiqué, Descartes délègue un de ses protégés, Jean Gillot, pour résoudre la question avec succès. Le dénombrement des solutions, une fois l'identité « de Brahmagupta » connue, est un exercice de combinatoire que plusieurs auteurs, comme Frenicle par exemple mènent aussi à bien. Reste la preuve que tout nombre premier de la forme 4k+1 est une somme de carrés parfaits. Or, il existe peu (voire pas du tout) de modèles de telles preuves d'existence dans un contexte arithmétique. L'interprétation géométrique des nombres entiers, à la base des preuves euclidiennes, est très lourde. Une solution consiste en une réinterprétation algébrique de ces problèmes : tout comme Stevin, François Viète, l'inventeur d'une des premiers symbolismes algébriques cohérents à grande échelle, a ainsi reformulé une grande partie des Arithmétiques de Diophante à la fin du XVI^e siècle. Mais, géométrie ou algèbre, comment garder trace du fait qu'on cherche ici des solutions entières ? Fermat est tout particulièrement conscient de cette difficulté  : dans un défi mathématique aux mathématiciens d' Europe, en 1657, il déclare : « À peine trouve-t-on qui pose des problèmes purement arithmétiques, ni qui les comprenne. N'est ce pas parce que jusqu'ici l'arithmétique a été traité géométriquement plutôt qu'arithmétiquement ? »

C'est dans le but de développer cette analyse diophantienne entière, avec des preuves, que Fermat a mis au point une méthode, celle qu'il nomme la descente infinie et qui, d'après ses dires, lui permet d'en venir à bout :

Je fus longtemps sans pouvoir appliquer ma méthode aux questions affirmatives, parce que le tour et le biais pour y venir est beaucoup plus malaisé que celui dont je me sers aux négatives. De sorte que, lorsqu'il me fallut démontrer que tout nombre premier, qui surpasse de l'unité un multiple de 4, est composé de deux quarrés, je me trouvai en belle peine. Mais enfin une méditation diverses fois réitérée me donna les lumières qui me manquoient, et les questions affirmatives passèrent par ma méthode, à l'aide de quelques nouveaux principes qu'il y fallut joindre par nécessité.

Fermat avait-il d'une démonstration complète de son théorème ? Aucune preuve rédigée par lui de ce théorème n'a subsisté. En revanche, les ingrédients qu'il a mis au point (petit théorème de Fermat, descente infinie) permettent effectivement d'en fabriquer une et plusieurs historiens se sont livrés à cet exercice de reconstruction.

Comme quelques autres, les premiers cas de son Grand Théorème en particulier, l'énoncé sur les sommes de deux carrés occupe en tout cas une place centrale dans le programme de Fermat pour rénover la théorie des nombres. Quatorze ans plus tard, bien après la mort de Mersenne, on voit réapparaître ces énoncés dans un projet d'ouvrage que Fermat adresse à Blaise Pascal, puis en 1658 au cours d'un échange avec les mathématiciens anglais, John Wallis et William Brouncker, et un an plus tard, dans un bilan sur la théorie des nombres destinée au jeune Christian Huygens. Fermat remarque aussi que des lois analogues peuvent être trouvées pour les nombres premiers x² + 2.y² = p et x² + 3.y² = p.

XVIII^e siècle : Preuves et extensions

L'environnement scientifique du siècle suivant est bien différent. Les mathématiques se sont professionnalisées partout en Europe et des journaux réguliers, en particulier les publications des diverses Académies des sciences, offrent la possibilité de publier au fur et à mesure résultats et preuves. Leonhard Euler s'est intéressé au théorème des deux carrés, comme à beaucoup d'autres résultats de théorie des nombres laissés par Fermat, et on lui doit les premières preuves connues de ces énoncés.

La référence géométrique à des triangles rectangles de côtés entiers disparait complètement au profit d'un formalisme purement algébrique. Euler étudie en particulier, à côté d'autres équations diophantiennes, les trois familles d'équations suivantes :

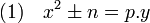
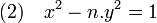
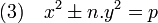
Ici, n désigne un nombre entier strictement positif et p un nombre premier. La dernière équation généralise celle associée au théorème des deux carrés (cas où n est égal à un).

En ce qui concerne le théorème des deux carrés, Euler montre d'abord qu'un nombre premier p = 4n − 1 ne divise pas une somme de deux carrés premiers entre eux, a² + b², en appliquant le petit théorème de Fermat. Il montre aussi qu'un diviseur d'une somme de deux carrés a² + b² est encore de cette forme (et donc s'il est premier, c'est soit 2 soit un entier de la forme 4n+1) ; ce résultat s'étend au cas de n=2 ou 3 (on trouve qu'un diviseur impair premier est congru à 1 ou 3 modulo 8 pour n=2 et à 1 modulo 3 pour n=3); dans ces derniers cas, la preuve inverse repose aussi sur des identités de puissances n-ièmes et le petit théorème de Fermat.

On trouve trace de ces résultats au fil de sa correspondance avec Christian Goldbach (qui contribue lui-même à cette étude), dès le début des années 1740, avec des publications détaillées, dans les Mémoires de l'Académie de Saint-Pétersbourg en particulier, une décennie plus tard. André Weil évoque cette période comme une « campagne de sept années » pour prouver toutes les assertions de Fermat sur les sommes de deux carrés ; jusque dans les années 1770, Euler y revient encore pour donner des variantes de ses preuves et de ces résultats.

Euler accumule aussi toutes sortes d'expérimentations numériques. Il conjecture dans ce contexte un résultat appelé à devenir une des lois centrales de la théorie des nombres, la loi de réciprocité quadratique, sans pouvoir le démontrer.

Reprenant une suggestion de Fermat, il interprète aussi le théorème sur les sommes de carrés comme un test de primalité. En effet, un nombre de la forme 4n + 1 est premier si et seulement s'il s'écrit d'une seule façon comme somme de deux carrés, et que ces carrés sont premiers entre eux. Ce critère permet à Euler de montrer que le 5^e nombre de Fermat, , n'est pas premier car il s'écrit de deux manières comme somme de carrés :

(2¹⁶)² + 1² = 62264² + 20449².

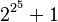
Euler cherche également à déterminer pour quels entiers μ,ν, l'étude des nombres représentables sous la forme μx² + νy² lui fournirait encore un critère de primalité analogue. Avec l'aide de ses assistants, il trouve que le critère marche lorsque le produit μν fait partie d'une liste de 65 nombres, qu'il baptise numeri idonei, nombres idoines. En utilisant le plus grand de ces nombres, 1848, Euler montre par exemple que 18518809( = 197² + 180480000) est premier.

Joseph-Louis Lagrange intègre les résultats tant théoriques que numériques d'Euler et les étend, dans un long mémoire en deux parties, intitulé « Recherches d'arithmétique ». Lagrange ne se limite pas à l'étude des nombres représentés par des sommes de carrés, mais étudie plus généralement les nombres entiers qui peuvent s'écrire sous la forme ax² + bxy + cy², pour des entiers x,y à trouver, les entiers a,b,c étant fixés. Une telle expression est appelée une forme quadratique binaire (c'est-à-dire du deuxième degré et à deux variables). Le théorème des deux carrés concerne la forme quadratique x² + y², c'est-à-dire celle pour laquelle a = c = 1,b = 0. Lagrange montre en particulier que deux formes f(x,y) et F(X,Y)représentent les mêmes entiers si un changement de variables x = αX + βY,y = γX + δY (avec des coefficients α,β,γ,δ entiers et tels que ) transforme l'une en l'autre, et que pour deux formes ainsi reliées, la quantité b² − 4ac, le discriminant de la forme, est identique. De telles formes seront appelées « équivalentes  » par Gauss quelques décennies plus tard et l'exploration de cette relation entre formes quadratiques par Lagrange constitue l'une des premières études connues d'une relation d'équivalence. Pour un discriminant donné, il n'y a qu'un nombre fini de classes de formes, à équivalence près.

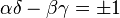
Lagrange remarque que les deux nombres entiers a et c sont représentés de manière primitive, c'est-à-dire avec des entiers x,y premiers entre eux par la forme quadratique ax² + bxy + cy² (puisque a = f(1,0),c = f(0,1), et aussi par toute forme équivalente ; réciproquement, il établit que tout nombre entier représentable de manière primitive par une forme est le coefficient du terme en X² pour une autre forme équivalente à la première, et que tout diviseur d'une forme est représentable par une forme de même discriminant (pas nécessairement équivalente). En particulier, si un nombre premier p divise la valeur en des entiers d'une forme quadratique, le discriminant D de la forme est un carré modulo p. La loi de réciprocité permet d'exprimer à l'inverse cette condition comme l'appartenance de p à certaines classes de congruence modulo la valeur absolue du discriminant (généralisant le fait que p doit être congru à 1 modulo 4 pour être représenté par une somme de carrés, c'est-à-dire une forme quadratique de discriminant -4).

Lagrange montre enfin comment, dans chaque classe de formes équivalentes, trouver des formes représentantes particulièrement simples : pour un discriminant négatif, il peut définir une forme représentante unique (dite forme réduite) par classe, pour un discriminant positif, la caractérisation des formes réduites fait appel à son étude sur l'équation (2) ci-dessus et aux fractions continues.

Adrien-Marie Legendre apporte sa pierre à l'édifice. Avant la fin du siècle, il introduit un symbole portant maintenant son nom permettant d'exprimer plus simplement la loi de réciprocité quadratique, même si la démonstration complète de cette loi lui échappe encore.

XIX^e siècle : nouveaux outils et nouveaux cadres

Au cours du XIX^e siècle, l'étude des problèmes sur les nombres entiers change de statut. D'une part, elle donne lieu à de vastes synthèses théoriques, unifiant de nombreuses questions jusqu'alors éparses. D'autre part, de marginale qu'elle était dans l'ensemble des mathématiques, elle devient l'objet de nombreuses interactions avec d'autres branches, comme la géométrie ou l'analyse réelle ou complexe. Le théorème des deux carrés bénéficie de ce double changement : il est intégré dans de nouveaux cadres, utilisé parfois comme une illustration des propriétés plus ou moins profondes mises à jour, et il est démontré plus directement, ou affiné, grâce à l'emploi de méthodes géométriques ou analytiques.

En 1801, Carl Friedrich Gauss publie un livre d'arithmétique novateur. La logique suivie consiste à étudier les nombres à l'aide d'une démarche structurelle. Il découvre que de multiple configurations, maintenant dénommées anneau euclidien bénéficiant des mêmes propriétés et donc d'une arithmétique analogue. Elle est parfois appelée arithmétique de l'horloge. De nouveaux ensembles de nombres sont étudiés, parfois de cardinal fini, parfois généralisant les entiers. Ces résultats offrent des démonstrations plus simples du théorème des deux carrés, permettent de prouver la loi de réciprocité quadratique et étendent la classification des formes quadratiques de Lagrange.

Les travaux de Gauss influencent les mathématiciens du siècle, Jacobi les utilisent pour établir une démonstration du nombre exact de décompositions d'un entier en deux carrés. Richard Dedekind , le dernier en date des élèves de Gauss, propose deux preuves à la fois élégantes et concises à l'aide des entiers de Gauss. Celle présentée dans cet article est la seconde.

Si les idées de Gauss permettent de mieux comprendre les nombres, le cas général reste hors de portée. Pour y arriver, il faudrait être capable de classifier toutes les formes quadratiques et les avancées du mathématicien sont insuffisantes. Cette classification suppose la connaissance des structures des extensions d'entiers, appelées entiers algébriques. Si ces ensembles disposent toujours d'une addition et d'une multiplication conférant une structure d'anneau, plus la valeur n augmente plus elle devient complexe. La division euclidienne disparait, puis, fait encore plus gênant, le théorème fondamental de l'arithmétique garantissant l'unicité de la décomposition en facteurs premiers s'évanouit à son tour.

Johann Peter Gustav Lejeune Dirichlet élucide la structure des éléments inversibles, Ernst Kummer trouve comment remplacer les facteurs premiers manquant à l'aide d'une notion maintenant appelé idéal, Evariste Galois ébauche une vaste théorie permettant de mieux comprendre comment les nombres se multiplient. Chacun des progrès, conséquence de l'œuvre de ses différents savants, permet de résoudre quelques cas supplémentaires. Le cas général n'est finalement résolu qu'à la dernière année du siècle grâce à la touche finale de David Hilbert .