Théorème du point fixe de Brouwer - Définition

Approche intuitive

Commentaires attribués à Brouwer

L'origine de ce théorème proviendrait de l'observation d'une tasse de café par Brouwer. Quand on mélange son sucre, il semble qu'il y ait toujours un point immobile. Il en déduit que : « À tout moment, il y a un point de la surface qui n'aura pas changé de place ». Le point fixe n'est pas nécessairement celui qui semble immobile car le centre du tourbillon bouge un petit peu. Le résultat n'est pas intuitif, car le point initialement fixe aura peut-être bougé, mais un autre point fixe apparaîtra.

Brouwer aurait ajouté : « Je peux formuler ce magnifique résultat autrement, je prends une feuille horizontale, une autre feuille identique que je froisse et que je replace en l'aplatissant sur l'autre. Un point de la feuille froissée est à la même place que sur l'autre feuille ». Quand Brouwer aplatit sa feuille froissée, il ne la déplie pas, il l'écrase, comme à l'aide d'un fer à repasser.

Dimension un

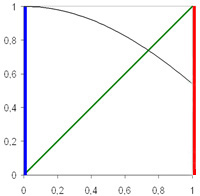
En dimension un, le résultat est à la fois intuitif et aisé à démontrer. On note [a, b] le domaine de définition de f. La fonction f est continue et à valeurs dans le même segment. Dire que cette fonction f admet un point fixe, revient à dire que son graphe (en noir sur la figure de droite et est choisi égal à celui de la fonction cosinus sur l'intervalle [0, 1]) croise celui de la fonction définie sur [a, b], qui à x associe x (en vert sur la figure de droite).

Intuitivement, une ligne (en noir) qui part d'un côté d'un carré (en bleu) pour rejoindre le côté opposé (en rouge) croise nécessairement les diagonales et en particulier la verte sur la figure.

Une démonstration n'est pas difficile à établir. Considérons la fonction continue g définie par :

Elle est positive en a, négative en b. Le Théorème de Bolzano, cas particulier du théorème des valeurs intermédiaires assure que la fonction g possède un zéro dans [a, b]. Ce zéro de g est un point fixe de f.

Brouwer aurait exprimé ce résultat de la manière suivante : « Au lieu d'examiner une surface, nous allons montrer le théorème sur un bout de ficelle. Partons d'un état de la ficelle bien dépliée, puis replions-la. Écrasons la ficelle repliée. Là encore un point de la ficelle n'a pas changé de place par rapport à sa position initiale sur la ficelle non repliée. ».

Dimension deux

En dimension deux, un raisonnement intuitif permet de montrer que le résultat est probablement vrai. La démonstration est néanmoins plus délicate. Si K, le domaine de définition de f est d'intérieur vide, c'est un segment. Sinon, K est semblable à une boule unité fermée. Le terme semblable signifie qu'il existe un homéomorphisme φ de la boule unité vers K. L'équation définissant le point fixe peut encore s'écrire, si h est égal à foφ, h(x) = x. Autrement dit, on peut supposer que K est la boule unité fermée. On peut de plus choisir la norme de manière quelconque. Si on choisit celle qui associe la valeur absolue de la plus grande coordonnée, cela revient à dire que l'on peut choisir pour compact K, l'ensemble [-1, 1]×[-1, 1], sans perte de généralité.

Si l'on définit la fonction g comme celle qui à x associe h(x) - x, cela revient à montrer que la fonction g atteint le vecteur nul sur [-1, 1]×[-1, 1]. Si g_k, pour k égal à 1 ou 2, sont les deux fonctions coordonnées de g, cela revient à montrer l'existence d'un point x₀, tel que g₁ et g₂ admettent toutes deux pour zéro la valeur x₀ .

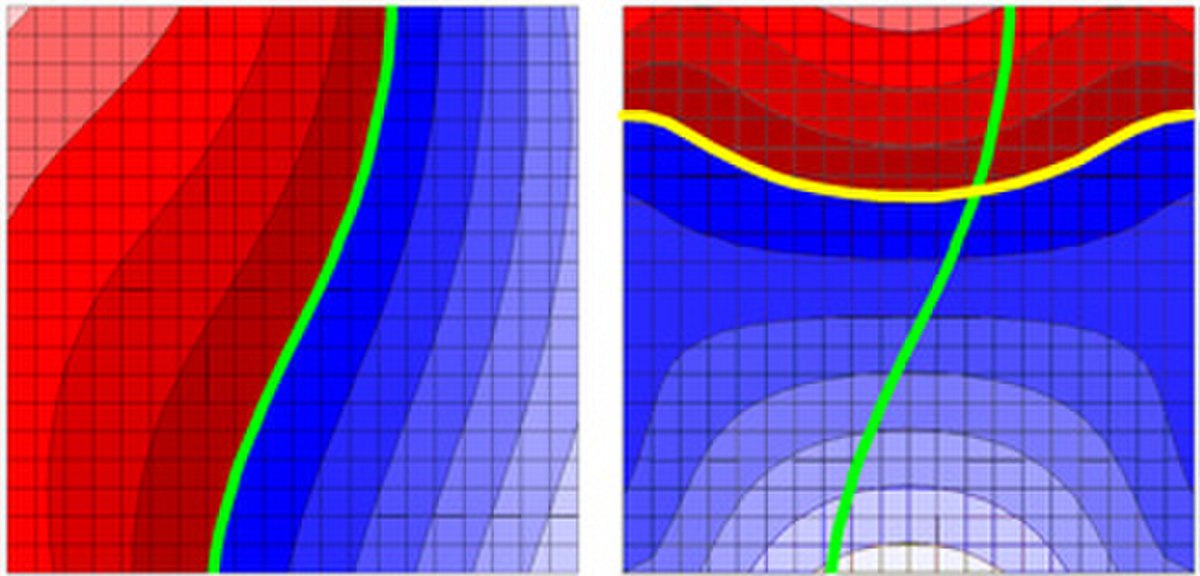
La fonction g₁ est une fonction de [-1, 1]×[-1, 1] dans [-1, 1]. Elle peut s'interpréter comme une carte d'une région, qui en chaque point donne l'altitude (illustrée sur la première figure à droite). Sur la zone {-1}×[-1, 1], cette altitude est positive (en rouge sur la figure), en revanche sur {1}×[-1, 1], elle est négative (en bleu sur la figure). Ceci laisse penser que la courbe de niveau 0 est une ligne (en vert sur la figure) qui part d'un point [-1, 1]×{1} pour finir sur un point de [-1, 1]×{-1}. Le même raisonnement appliquée à g₂ laisse penser que la courbe de niveau 0 est cette fois-ci une ligne qui part d'un point de {-1}×[-1, 1] pour terminer sur un point de {1}×[-1, 1] (illustré sur la deuxième figure, la ligne est en jaune).

Intuitivement, il semble évident que ces deux lignes de niveaux (en vert et en jaune) doivent nécessairement se croiser et ce point de croisement est un point fixe de foφ. Démontrer cette intuition est moins aisée qu'il n'y parait. La zone verte n'est pas nécessairement une ligne connexe, ni même une ligne, même si elle en contient toujours une. Elle peut être, par exemple, une bande.

Dimension finie

L'approche intuitive du paragraphe précédent se généralise à toute dimension finie. Pour s'en persuader, étudions le cas de la dimension 3.

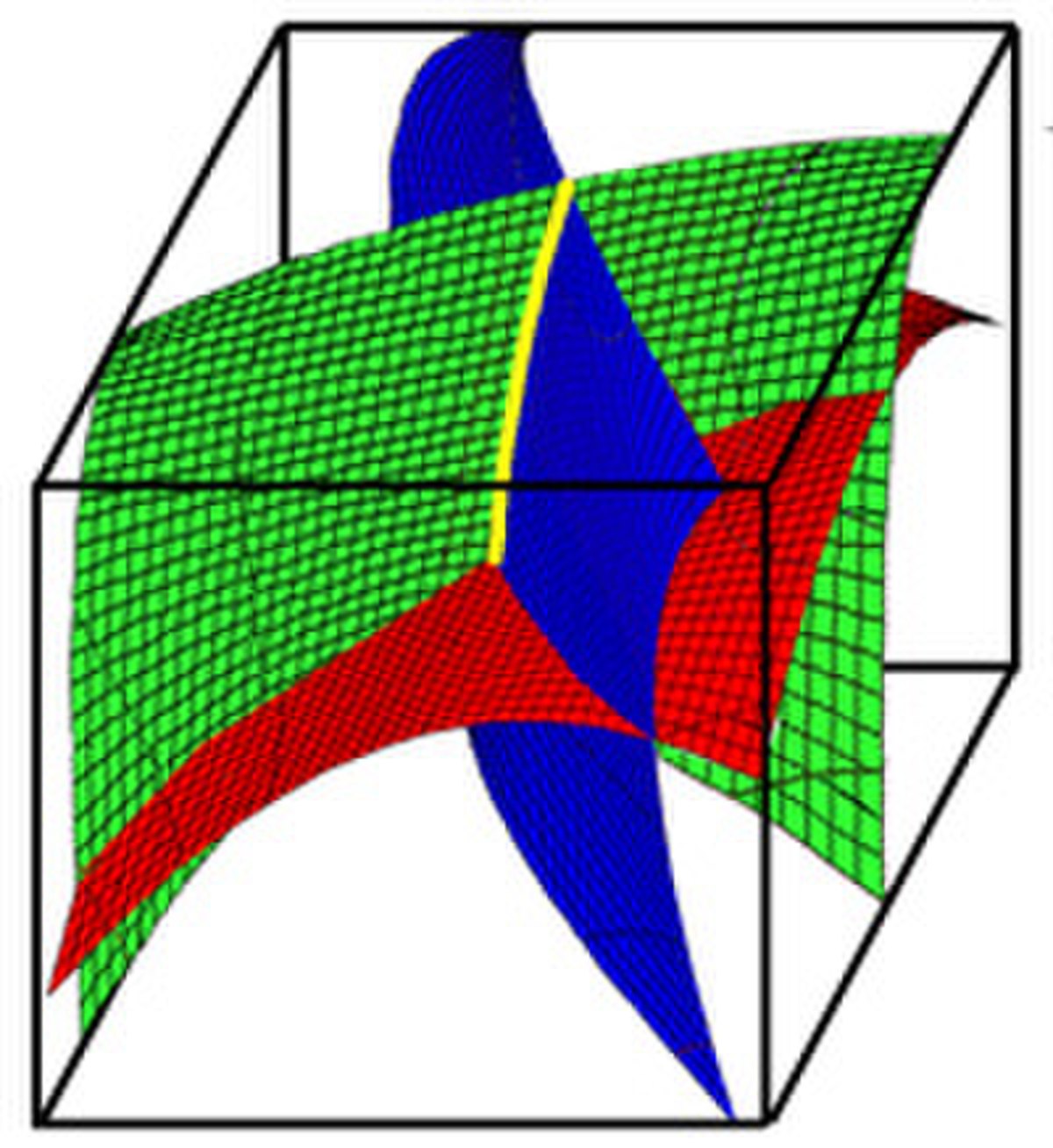
L'objectif est toujours de montrer l'existence d'un zéro de la fonction g, qui maintenant possède trois coordonnées. La première coordonnée est positive sur la face gauche du cube et négative sur la face droite. Il y a tout lieu de penser que la zone des zéros contient une nappe, illustrée en bleu sur la figure de droite. Cette nappe coupe le cube en au moins deux composantes connexes, l'une contenant une portion de la face de droite l'autre celle de gauche.

Si l'axe des y décrit la direction devant-derrière le même raisonnement laisse penser à l'existence d'une nappe, en vert sur la figure, qui coupe encore en au moins deux composantes connexes le cube. L'intersection des deux nappes contient probablement une ligne, en jaune sur la figure, partant de la face du haut pour rejoindre celle du bas.

La troisième composante de g décrit cette fois-ci, une nappe en rouge sur la figure. Cette nappe semble croiser nécessairement la ligne jaune. Ce point d'intersection est un point fixe recherché.