Théorème du point fixe de Brouwer - Définition

Introduction

En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L'énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910. Luitzen Brouwer propose une nouvelle démonstration en 1912.

En mathématiques, le théorème du point fixe de Brouwer est un résultat de Topologie algébrique. Il fait partie de la grande famille des théorèmes de point fixe, qui énoncent que si une fonction continue f vérifie certaines propriétés, alors il existe un point x₀ tel que f(x₀) = x₀. La forme la plus simple du théorème de Brouwer prend comme hypothèse que la fonction f est définie dans un intervalle fermé borné I et à valeurs dans I. Sous une forme plus générale, la fonction est définie dans un convexe compact K d'un espace euclidien et à valeurs dans K.

Si, parmi les centaines de théorèmes de point fixe, celui de Brouwer est particulièrement célèbre, c'est en partie parce qu'il est utilisé dans de nombreuses branches mathématiques. Dans sa branche d'origine, ce résultat est l'un des théorèmes clés caractérisant la topologie d'un espace euclidien, comme le théorème de Jordan, celui de la boule chevelue ou de Borsuk-Ulam. À ce titre, il est un des théorèmes fondamentaux de la topologie. Ce théorème intervient aussi pour établir des résultats fins sur les équations différentielles ; il est présent dans les cours élémentaires de géométrie différentielle. Il apparaît dans des branches plus inattendues, comme la théorie des jeux, où John Nash l'utilise pour montrer l'existence d'un équilibre pour un jeu de n personnes avec stratégies mixtes. Historiquement, le théorème est étudié à la suite de travaux sur les équations différentielles de mathématiciens français comme Poincaré et Picard. Démontrer des résultats comme le théorème de Poincaré-Bendixson demande l'usage d'outils de topologie. Ces études de la fin du XIX^e siècle débouchent sur plusieurs versions successives du théorème ; en 1912, Luitzen Egbertus Jan Brouwer en propose une démonstration générale, établissant à nouveau un résultat déjà prouvé par Hadamard en 1910.

Énoncés

Il existe plusieurs formes du théorème, selon le contexte d'utilisation. La plus simple est parfois donnée sous la forme suivante :

Il est possible de généraliser à toute dimension finie.

Il peut encore être un peu plus général :

On trouve une forme encore plus générale, mais habituellement, elle porte alors un autre nom :

Fragments d'histoire

Préhistoire

Si la zone parcourue par le courant n'est pas bornée, ou contient un trou en son milieu, le théorème ne n'applique pas.

Dans le cas d'une zone ayant la forme d'un disque, le théorème s'applique et garantit l'existence d'un point fixe.

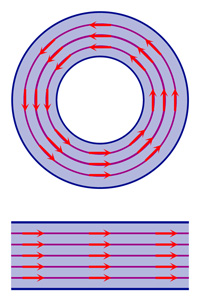
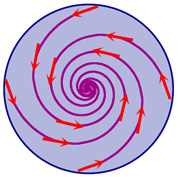
Comprendre la préhistoire du théorème du point fixe de Brouwer impose un passage par une équation différentielle. À la fin du XIX^e siècle, une vieille question focalise à nouveau l'attention de la communauté mathématique, celle de la stabilité du système solaire. La résoudre suppose la mise au point de nouvelles méthodes. Comme le fait remarquer Henri Poincaré, qui étudie le problème des trois corps, la recherche d'une solution exacte est vaine : « Rien n’est plus propre à nous donner une idée de la complication du problème des trois corps et en général de tous les problèmes de Dynamique où il n’y a pas d’intégrale uniforme et où les séries de Bohlin sont divergentes ». Ce mathématicien remarque aussi que la recherche d'une solution approchée n'est pas plus efficace : « plus nous cherchons à obtenir des approximations précises et plus le résultat va diverger vers une imprécision croissante ».

Il étudie une question analogue à celle du mouvement de la surface d'une tasse de café. Que peut-on dire, en général, des trajectoires d'une surface animée par un courant constant? Poincaré découvre que la réponse réside dans ce que l'on appelle maintenant les propriétés topologiques de la zone contenant la trajectoire. Si cette zone est compacte, c'est-à-dire à la fois fermée et bornée, soit la trajectoire s'immobilise, soit elle s'approche de plus en plus d'une boucle qu'elle parcourt indéfiniment. Poincaré va plus loin, si la zone est de même nature que celle d'un disque, comme c'est le cas pour la tasse de café, il existe nécessairement un point fixe. Ce point fixe est invariant par toutes les fonctions qui, à chaque point de la surface initiale, associent sa position au bout d'une période t. Si cette zone correspond à une bande circulaire ou si elle n'est pas fermée, ce n'est pas nécessairement le cas.

Pour mieux comprendre l'équation différentielle, une nouvelle branche des mathématiques voit le jour. Poincaré l'appelle l'analysis situs, L'Encyclopedia Universalis la définit comme celle qui « concerne les propriétés invariantes d’une figure lorsqu’on la déforme de manière continue quelconque, sans déchirure (par exemple, dans le cas de la déformation de la sphère, les propriétés corrélatives des objets tracés sur sa surface ». Dès 1886, Poincaré établit un résultat équivalent au théorème du point fixe de Brouwer, mais le rapport avec le thème de cet l'article n'est pas fait. Un peu plus tard, il développe l'un des outils de base pour mieux comprendre l'analysis situs, que l'on appelle maintenant le groupe fondamental ou le groupe de Poincaré. Cette méthode est utilisée dans une des démonstrations du théorème présentées dans l'article.

Par certains côtés, l'approche de Poincaré est analogue à celle d'Emile Picard, un mathématicien contemporain qui généralise le théorème de Cauchy-Lipschitz. La démarche de Picard s'appuie sur un résultat qui sera formalisé plus tard par un autre théorème du point fixe, dit de Banach. Ce théorème ne s'appuie pas sur les propriétés topologiques du domaine de définition, mais sur le fait que la fonction étudiée est contractante.

Premières démonstrations

Hadamard joue un rôle d'accoucheur auprès de Brouwer pour lui permettre de formaliser ses idées.

À l'aube du XX^e siècle, l'intérêt de l'analysis situs, n'est pas passé inaperçu. En revanche, la nécessité d'un théorème équivalent à celui de l'article n'est pas encore évidente. Piers Bohl, un mathématicien letton applique des méthodes topologiques pour étudier des équations différentielles. Il démontre en 1904 le résultat de l'article pour la dimension trois, son texte passe inaperçu.

C'est finalement Brouwer, qui donne à ce théorème ses premières lettres de noblesse. Ses objectifs sont différents de ceux de Poincaré. Ce mathématicien est passionné par les fondements des mathématiques, essentiellement la logique et la topologie. Son intérêt initial réside dans une tentative de résolution du cinquième problème de Hilbert. En 1909, lors d'un voyage à Paris, il rencontre Poincaré, Hadamard et Borel. Les discussions qui s'en suivent convainquent Brouwer de l'importance de mieux comprendre la topologie des espaces euclidiens et est l'origine d'une fructueuse relation épistolaire avec Hadamard. Durant les quatre années à venir, il se concentre pour établir certains grands théorèmes sur cette question. Cette année là, Brouwer démontre le théorème de la boule chevelue pour la sphère de dimension deux, ainsi que le fait que toute application continue de la boule de dimension deux dans elle même possède un point fixe. Ces deux résultats en eux-mêmes ne sont pas véritablement des nouveautés. Comme lui fait remarquer Hadamard, un équivalent du théorème de la boule chevelue est déjà démontré par Poincaré. L'aspect révolutionnaire de l'approche de Brouwer consiste en l'usage systématique d'outils développés récemment comme l'homotopie, le concept de base du groupe de Poincaré. L'année suivante, Hadamard généralise le théorème de l'article à toute dimension finie, mais à l'aide de méthodes différentes. Hans Freudenthal commente ainsi les rôles respectifs : « Comparées aux méthodes révolutionnaires de Brouwer, celles d'Hadamard sont très traditionnelles, mais la participation d'Hadamard à la naissance des idées de Brouwer ressemble plus à celle d'une sage-femme qu'à celle d'un simple spectateur ».

L'approche de Brouwer porte ses fruits, en 1912 il trouve aussi une démonstration valable pour toute dimension finie, ainsi que d'autres théorèmes clé comme l'invariance de la dimension. Dans le contexte de ces travaux, Brouwer généralise aussi le théorème de Jordan à une dimension quelconque et établit les propriétés associées au degré d'une application. Cette branche des mathématiques, initialement imaginée par Poincaré et développée par Brouwer, change de nom. Dans les années 1930, l'analysis situs devient la topologie algébrique.

La célébrité de Brouwer n'est pas uniquement la conséquence de ses travaux en topologie. Il est aussi auteur et ardent défenseur d'une manière de formaliser les mathématiques, appelée intuitionnisme, qui, à l'époque se voulait opposé au formalisme de la théorie des ensembles. Si Brouwer préfère des preuves fondées sur une démonstration constructive, ironiquement, celles à l'origine de ses grands théorèmes de topologie ne le sont pas et il faut attendre 1967 pour en trouver.

Postérité du théorème

John Nash utilise le théorème en théorie des jeux pour démontrer l'existence d'une stratégie gagnante.

Le théorème de l'article s'avère fondamental, au moins à deux titres. Le XX^e siècle développe de nombreux théorèmes de point fixe, et même une théorie sur cette question. Celui de Brouwer est probablement le plus important. Il est aussi l'un des théorèmes fondateurs de la topologie des variétés topologiques et est souvent utilisé pour la démonstration des autres résultats importants, comme le théorème de Jordan.

Par delà les théorèmes de point fixe dont l'origine est une fonction plus ou moins contractante, ceux directement ou indirectement issus du résultat de l'article sont nombreux. Il n'existe pas d'application continue d'une boule fermée d'un espace euclidien dans sa frontière, laissant invariant sa frontière. Dans le même ordre d'idée, le théorème de Borsuk-Ulam indique qu'une application continue de la sphère de dimension n dans Rⁿ possède au moins deux points antipodaux de même image. Dans le cas de la dimension finie, le théorème du point fixe de Lefschetz, établit en 1926 une méthode pour compter les points fixes. Le théorème du point fixe de Brouwer est généralisé en 1930 aux espaces de Banach. Cette généralisation porte le nom de théorème du point fixe de Schauder, résultat encore généralisé par S. Kakutani aux fonctions multivoques. On ne rencontre pas uniquement le théorème ou ses avatars en topologie. Le théorème de Hartman-Grobmann, qui établit la nature qualitative du comportement de certaines équations différentielles au voisinages de certains points d'équilibre, se démontre avec le résultat de l'article. Sur le même sujet, le théorème de la variété centrale utilise aussi le théorème du point fixe de Brouwer pour sa démonstration. On trouve encore le théorème pour démontrer des existences de solutions à certaines équations aux dérivées partielles.

D'autres domaines sont touchés. En théorie des jeux, John Nash utilise ce théorème pour prouver qu'au jeu de Hex, il existe une stratégie telle que les blancs jouent et gagnent. En économie, P. Bich précise que certaines généralisations du théorème montrent que son usage est utile pour « quelques problèmes classiques en théorie des jeux ou en équilibre général (modèle d’Hotelling, équilibres financiers en marchés incomplets, ..)  ».