Théorème du point fixe de Brouwer - Définition

Démonstrations

Préambule

Les méthodes de démonstrations sont nombreuses. L'une particulièrement simple est l'œuvre de David Gale. Elle provient d'une analyse différente des résultats de Nash sur le jeu de Hex. La preuve présentée ici s'applique à la dimension deux, mais l'article original ne contient pas cette limitation.

La topologie combinatoire est une autre méthode permettant de démontrer le théorème. Pendant les années 1920, les mathématiciens ont commencé à dégager des principes combinatoires liés au théorème de Brouwer (lemme de Sperner, lemme de Knaster–Kuratowski–Mazurkiewicz). Ces travaux offrirent à la fois de nouvelles démonstrations élégantes de ce théorème et l'amorce d'une théorie en combinatoire pour l'avenir.

D'autres utilisent la géométrie différentielle. Milnor établit un lemme qui simplifie la preuve pour les fonctions infiniment différentiables. Il devient aisé de conclure pour les fonctions continues à l'aide du théorème de Stone-Weierstrass. L'usage de théorèmes puissants rend la démonstration plus facile. En géométrie différentielle, le théorème de Stokes implique directement celui du point fixe de Brouwer, pour les fonctions de classe C². Une autre méthode consiste à faire appel à des théorèmes un peu équivalents, comme celui de la boule chevelue ou de Borsuk-Ulam.

Néanmoins, pour Daniel Leborgne, les théorèmes comme celui du point fixe de Brouwer « sont habituellement démontrés par des méthodes universelles de topologie algébrique, donc, évidemment préférables ». En dimension deux, une preuve présentée ici utilise le groupe de Poincaré, qui se fonde sur la notion d'homotopie. Pour une dimension quelconque, la preuve se généralise, la notion clé n'est plus l'homotopie mais l'homologie.

Par le jeu de Hex

Fin d'une partie de jeu de Hex. Bleu a gagné.

En 1949, Nash réinvente le jeu de Hex et montre que la partie nulle y est impossible. Sa démonstration est équivalente au théorème de l'article. Une trentaine d'années plus tard, D. Gale s'en rend compte et montre que le jeu peut servir de démonstration élémentaire au résultat de Brouwer.

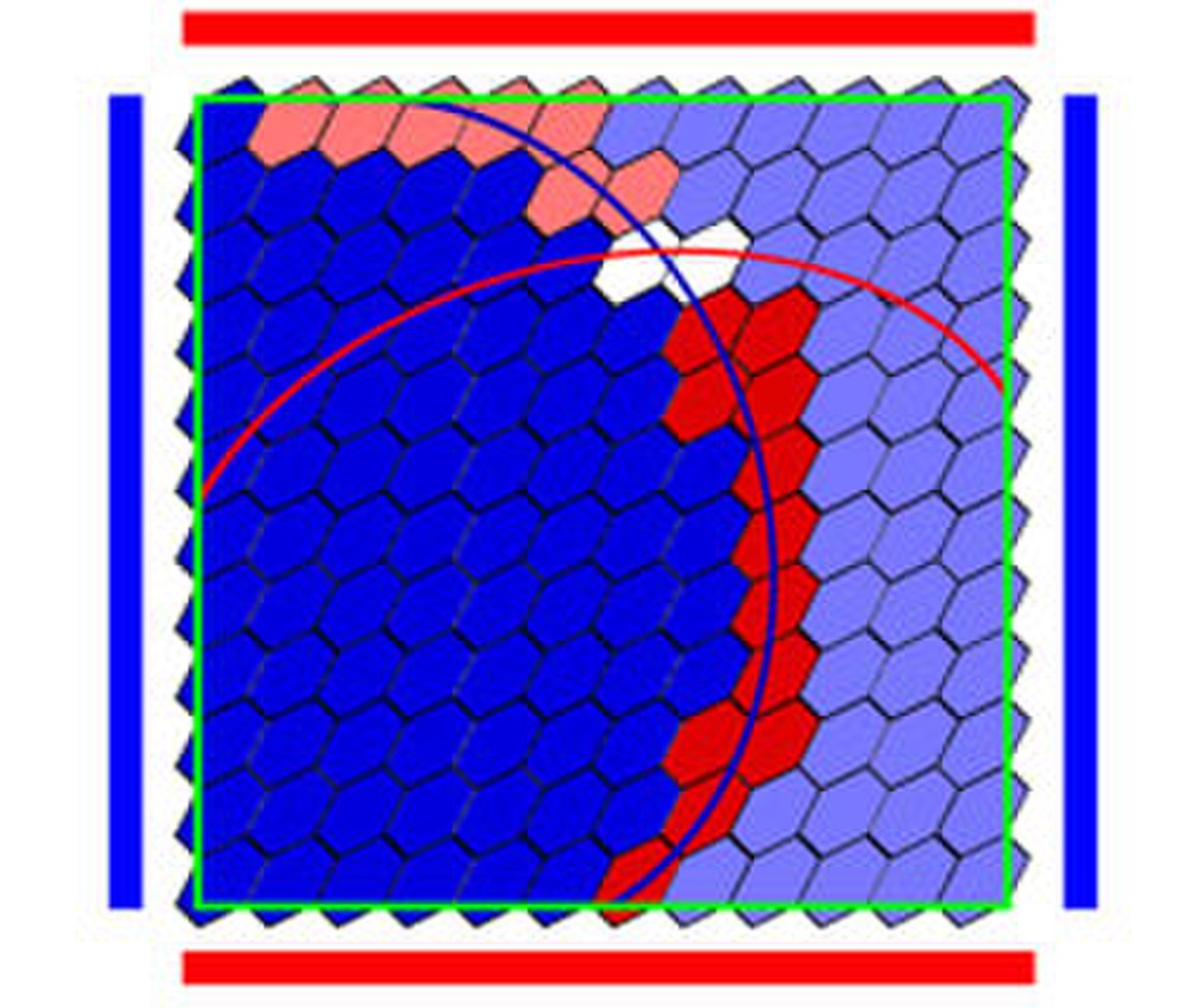
Le jeu a lieu sur un plateau composé d'hexagones. À la fin du jeu, certains hexagones sont recouverts par des jetons (rouges ou bleus sur la figure de gauche). Le camp des bleus est formé par deux côtés de l'hexagone signalés par une ligne bleue, les deux autres côtés (signalés par une ligne rouge) constituent le camp adverse. S'il est possible de tracer une ligne blanche qui ne quitte jamais la zone des hexagones bleus et qui relie les deux côtés bleus, les bleus ont gagné, comme illustré sur la figure de gauche. De même, s'il est possible de tracer une ligne blanche qui ne quitte jamais la zone des hexagones rouges et qui relie les deux côtés rouges, les rouges ont gagné. L'article Hex montre que si le plateau est rempli de jetons, le match nul est impossible, c'est-à-dire que, soit les hexagones rouges, soit les bleus, sont support d'une ligne blanche reliant les deux côtés d'un même camp. Cette propriété permet de démontrer le théorème de Brouwer.

On prouve ici le théorème de Brouwer, pour le compact convexe de R², K étant égal à [-1, 1]×[-1, 1], c'est-à-dire que la norme choisie ||.|| est celle de la plus grande valeur absolue de ses deux coordonnées. En dernière partie du paragraphe sur les démonstrations, on montre que ce résultat suffit à prouver le théorème de Brouwer pour n'importe quel compact convexe de R². L'article de D. Gale montre que le raisonnement se généralise à une dimension quelconque, ce qui n'est pas fait ici.

Soit f une fonction continue de K dans K. La fonction g est celle définie de K dans K, qui à x associe f(x) - x. Démontrer le théorème de Brouwer revient à montrer que g admet un zéro. Ce résultat ce prouve à l'aide du lemme suivant :

Une fois ce lemme démontré, on remarque que la continuité de f implique celle de ||g|| et, comme elle est définie dans un compact, elle est uniformément continue. Comme K est un compact, la fonction ||g|| atteint son minimum en un point que l'on note m. Ce minimum est un entier positif strictement plus petit que ε. Le seul réel positif plus petit que tous les réels strictement positifs est 0. L'image par g du point m est donc nulle, ce qui démontre le théorème.

Comme la fonction g est uniformément continue, il existe un réel strictement positif δ tel que :

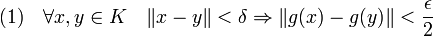
Le compact K, dont la frontière est illustrée en vert sur la figure de droite, est rempli par un plateau de hex redressé (cf l'image de droite). Le plateau contient suffisamment d'hexagones pour que chacun puisse être contenu dans un disque de diamètre δ. On note g₁ et f₁ (resp. g₂ et f₂) la première (resp. la deuxième) coordonnée des fonctions g et f. En faisant jouer au hex, les fonctions g₁ et g₂, on démontre le lemme.

Soit B_f l'ensemble des hexagones tels que g₁ soit strictement supérieure à ε/2 sur l'intégralité de l'hexagone. Ces hexagones sont dessinés en bleu foncé sur la figure. On considère les hexagones recouvrant la zone {1}x[-1, 1] et x un élément de cette zone. La fonction g₁ au point x vaut f₁(x) - 1 c'est-à-dire un nombre nécessairement négatif. Ceci montre qu'aucun hexagone contenant un point de {1}x[-1, 1] ne peut être bleu foncé. Soit B_c l'ensemble des hexagones tel que g₁ soit strictement inférieure à -ε/2 sur l'intégralité de l'hexagone. Ces hexagones sont dessinées en bleu clair sur la figure. Le raisonnement précédent montre que la zone {-1}x[-1, 1] ne peut contenir aucun hexagone bleu clair.

Cet argument montre que si les hexagones bleus, clairs ou foncés, représentent les pions d'un joueur, ce joueur ne peut avoir gagné. L'argument précédent montre qu'il n'existe aucune possibilité d'une suite connexe d'hexagones bleus uniquement clairs ou uniquement foncés reliant les deux bords. Or deux hexagones bleus, l'un clair et l'autre foncé, ne peuvent être connexes. Ils partageraient une arête sur laquelle la fonction g₁ serait à la fois strictement positive et strictement négative.

On définit de même R_f (resp. R_c l'ensemble des hexagones qui ne sont pas bleus et tels g₂ soit strictement supérieur à ε/2 (resp. inférieur à -ε/2) sur tout l'hexagone. Le même raisonnement précédent montre que les hexagones rouges (union des R_f rouge foncé et R_c rouge clair) ne représentent pas non plus une configuration gagnante.

Le résultat, montré dans l'article hex, permet de déduire qu'il existe un hexagone qui n'est ni rouge ni bleu. Par définition, un tel hexagone contient un point x dont l'image par g₁ est, en valeur absolue plus petite que ε/2, et un point y dont l'image par g₂ est, en valeur absolue aussi plus petite que ε/2. Comme x et y sont situés à une distance plus petite que δ l'un de l'autre, les valeurs de g(x) et de g(y) sont, en valeurs absolues, plus petite que ε, d'après la majoration (1).

 

Par une méthode homotopique

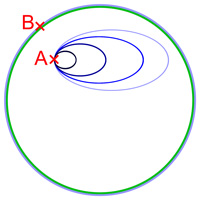
Les raisonnements les plus généraux pour les démonstrations du théorème sont issus de la topologie algébrique. Ici, il est plus simple d'identifier le cercle avec les points du plan complexe de module 1 et le disque avec les points de modules inférieurs ou égaux à 1. Il existe une différence topologique entre le disque et le cercle. Soit un point A du disque et un lacet d'extrémités A, c'est-à-dire un chemin continu qui part de A, sans jamais quitter le disque, pour retourner au point A. Si le lacet est matérialisé par un fil élastique, on peut tirer sur chacune des extrémités du chemin pour finir par un chemin composé d'un point unique : A. Autrement dit, on peut déformer continument le lacet jusqu'à n'obtenir qu'un point. Cette propriété est illustrée sur la figure de droite, le lacet bleu est continument déformé pour obtenir un chemin de plus en plus proche du lacet constant égal à A. On dit que tout lacet est homotope à un point. Sur le cercle, cette propriété n'est pas vraie. On peut imaginer un chemin qui part du point B, fait le tour du cercle et revient en B. On obtient un lacet d'extrémités B et qui parcourt le cercle. Cette fois-ci, on aura beau tirer sur le chemin ou le fil élastique, qui ne peut par définition par quitter le cercle, il n'y aura pas moyen de le ramener au point B sans le rompre. En termes mathématiques, on dit que le groupe fondamental du disque est trivial, alors que celui du cercle ne l'est pas.

Si une exception au théorème de Brouwer existait, il serait possible de créer un lacet qui ferait le tour du cercle en allant toujours dans la même direction, et qui serait pourtant homotope à un point. Cette impossibilité est la clé de la démonstration proposée ici. Dans un premier temps, on démontre la propriété suivante :

• Il n'existe pas de fonction continue du disque dans le cercle, qui laisse invariant le cercle.

Ce qui se dit encore : il n'existe pas de rétraction continue du disque dans sa frontière. En effet, S'il y en avait une que l'on note F, on définirait la fonction H par :

Si x est égal à 1, on obtient un lacet d'extrémités le point 1 et qui fait le tour du disque, si t varie. Si x est égal à 0, on obtient un lacet constant de valeur F(0). Le lacet initial serait homotope à un point, comme cette propriété est fausse dans le cercle, la proposition est démontrée. L'article détaillé propose une démarche plus rapide, elle suppose néanmoins l'acquisition de concepts plus lourds à mettre en œuvre.

Il reste encore à construire la fonction F.

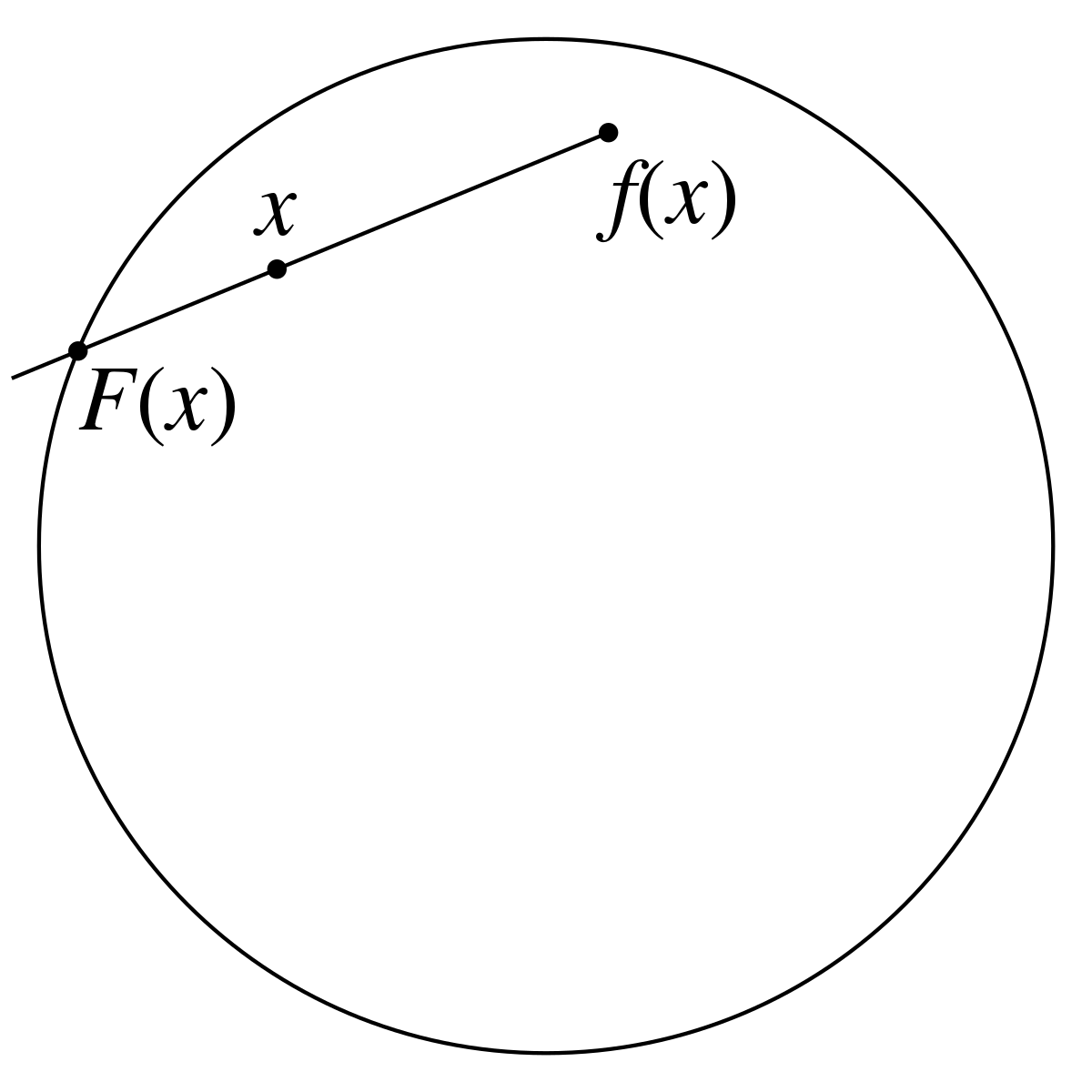
• S'il existe une fonction continue f du disque dans lui-même sans point fixe, il existe une rétraction continue F du disque dans sa frontière.

On considère le segment passant par x et f(x) et d'extrémités f(x) et un point du cercle. Cette construction est illustrée sur la figure de droite. Comme x et f(x) ne sont jamais confondus, la fonction F est parfaitement définie. Si x est sur la frontière, les points x et F(x) sont confondus. Il est relativement simple de montrer que F est continue.

Le lacet α est celui qui à t, élément de [0, 1], associe exp(2πi.t). Il n'est pas homotope au lacet c constant toujours égal à 1. Cette vérité est en général démontrée dans un résultat plus large, établissant la structure du groupe fondamental du cercle. On peut néanmoins procéder plus directement. Intuitivement, si le lacet s'imagine comme un fil qui tourne autour du cercle, tirer suffisamment fort sur les deux brins que l'on trouve au point 1 pour ramener l'intégralité du fil en 1, va casser le fil. Trouver le point de cassure est une méthode pour exhiber une discontinuité. Cette propriété permet d'établir le résultat suivant.

• Il n'existe pas de rétraction continue du disque dans le cercle :

On raisonne par l'absurde et l'on suppose qu'il existe une telle rétraction F. On considère la fonction H(t, x) de [0, 1]² dans le cercle, définie par :

Si x est égal à 1, comme la rétraction est la fonction identité sur le cercle, le lacet qui à t associe H(t, 1) est bien égal à α. Si x est égal à 0, la fonction qui à t associe H(t, 0) est constante. Comme la fonction H est continue, on aurait montrer que le lacet α est homotope à un point. La rétraction ne peut donc exister, d'après la première proposition.

• Si une fonction f du disque dans lui même est sans point fixe et continue, il existe une rétraction continue F du disque dans le cercle :

La fonction F est définie comme indiqué précédemment. Il faut encore montrer qu'elle est continue. On cherche le point appartenant au cercle unité et à la demi-droite d'origine x et dirigée par le vecteur x - f(x). Ce point est l'image d'une valeur positive (ou nulle) de t par la fonction qui à t, associe x + t(x - f(x)). Plus exactement, t est l'unique racine positive du polynôme P(t), défini par (||.|| désigne la norme euclidienne) :

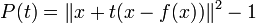
Ce polynôme est du second degré et s'écrit encore a(x)t² + b(x)t + c(x), ici a(x), b(x) et c(x) désignent trois fonctions continues définies sur le disque et à valeurs dans R. On remarque que le coefficient du monôme dominant a(x) est toujours strictement positif (car x est différent de f(x) d'après les hypothèses retenues) et les images du polynôme en 0 et en -1 sont négatives. Un tel polynôme admet toujours une unique racine positive et elle s'écrit comme une fonction, notée λ, continue des trois coefficients a(x), b(x) et c(x). On en déduit que λ est une fonction continue de x et la rétraction F(x), qui s'écrit :

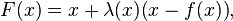
est aussi continue.

 

Par le théorème de la boule chevelue

Le théorème de la boule chevelue énonce que sur une sphère unité de dimension paire (c'est-à-dire la sphère de rayon 1 et de centre le vecteur nul, dans un espace euclidien de dimension impaire), il n'existe pas de champ de vecteurs α qui soit continu, orthogonal à la sphère en tout point x de cette sphère (c'est-à-dire vérifiant (x|α(x)) = 0), et qui ne s'annule jamais. On l'exprime parfois en disant qu'il existe toujours un point de la Terre où le vent est inexistant.

S'il existe une fonction f de la boule unité fermée B_n sans point fixe, il existe une méthode astucieuse^{[réf. souhaitée]} permettant de construire deux champs de vecteurs, sur la sphère unité de dimension n et celle de dimension n +1 , dont l'un des deux contredit le théorème de la boule chevelue. L'avantage de cette méthode est qu'elle n'utilise que des techniques élémentaires, sa faiblesse réside dans une démarche moins universelle que celle de la topologie algébrique, qui permet de démontrer aussi les autres résultats un peu équivalents, comme le théorème de Borsuk-Ulam.

Notons S_n-1 la sphère unité de Rⁿ, ou encore la frontière de B_n. La démonstration est par l'absurde et en trois étapes :

1. s'il existe une application continue f sans point fixe de B_n dans lui-même, il en existe aussi une g de B_n+1 dans lui-même ;
2. s'il existe une application continue sans point fixe de B_m dans lui-même, il existe sur la sphère S_m un champ α de vecteurs non nuls tel que (x|α(x)) = 0 pour tout x de cette sphère ;
3. en appliquant la deuxième étape à f, et au g déduit de f par la première étape, on obtient deux champs de vecteurs (l'un sur S_n, l'autre sur S_n+1), qui d'après le théorème de la boule chevelue prouvent que n n'est ni pair, ni impair, d'où la contradiction souhaitée.

Il reste à détailler les deux premières étapes.

• Etape 1.

En utilisant que B_m est homéomorphe à [-1,1]^m (pour m=n et pour m=n+1), on se ramène à démontrer que s'il existe une application continue F sans point fixe de [-1,1]ⁿ dans lui-même, il en existe aussi une G de [-1,1]ⁿ⁺¹ dans lui-même.

L'assertion devient ainsi immédiate : il suffit de poser G(x,t)=(F(x),t), pour tout x de [-1,1]ⁿ et tout t de [-1,1].

• Etape 2.

Soit h une application continue sans point fixe de B_m dans lui-même. Posons

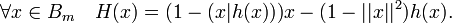
Du fait que h est sans point fixe on déduit que pour x intérieur à la boule, H(x) est non nul, et que pour x sur la sphère on a même (x|H(x))=1-(x|h(x))>0.

Posons ensuite, en désignant par x les m premières coordonnées d'un vecteur X de R^m+1 et par t sa dernière coordonnée :

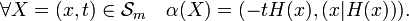
Manifestement, la fonction α est continue et vérifie (X|α(X)) = 0. Enfin, α(X) n'est jamais nul (car si x est de norme 1, (x|H(x)) est non nul, et si x est de norme strictement inférieure à 1, t et H(x) sont non nuls).