Théorie de Galois à l'origine - Définition

La théorie de Galois en détail

Préliminaires

Si K est un corps, on appelle sa clôture algébrique. Pour une partie A de on appelle le plus petit sous-corps de contenant K et A. On dira pour que x se déduit rationnellement de A (parfois K sera précisé, si ce n'est pas le cas ce sera souvent le corps engendré par les coefficient du polynôme).

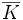
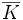
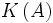
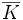
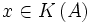
Soit P un polynôme. Par exemple . On remarquera que si l'on appelle ses trois racines , et . Alors ce polynôme s'écrit aussi . On remarquera que les coefficients s'expriment à l'aide de polynômes symétriques en les racines.

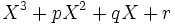
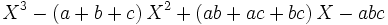
Théorème de l'élément primitif

Soit, , un polynôme irréductible. Si l'on prend un polynôme en ses racines tel qu'il décrive des valeurs différentes pour toutes les permutations de ses racines alors, si l'on appelle V l'une de ces valeurs, chacune des racines du polynôme se déduit rationnellement de V.

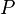
Preuve

• L'existence du polynôme décrivant des valeurs différentes est à faire.

• Soit le degré du polynôme . On appelle , où sont les racines du polynôme . L'expression , est invariante pour toutes les permutations des racines autres que la première et peut donc s'exprimer en un polynôme en et , que l'on notera . On remarque que le polynôme ne s'annule qu'en . En applicant l'algorithme d'Euclide pour trouver son pgcd avec on obtiendra un polynôme du premier degré dont la racine est . On peut donc exprimer rationnellement en fonction de . On fait de même avec les autres racines.

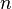
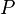
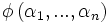
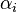
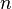
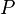
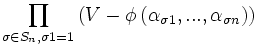
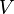
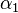
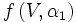
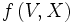
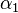
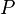
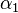
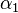
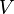
Q.E.D

Groupe du polynôme

Il existe un groupe de permutation des racines qui laisse toute quantité rationnellement connu invariable. Et tel que toute autre permutation des racines change ces quantités.

Preuve

• Soit le polynôme irréductible de . On appellera donc les racines de . On a vu que chacune des racines de s'exprimait rationnellement en fonction de . Appelons l'expression qui donne en fonction de . On remarque que est aussi une racine du polynôme . Ainsi pour chaque on a les racines du polynômes dans un certain ordre et pour un autre dans un autre autre ordre. Toutes les permutations qui nous permettent de passer d'un ordre à l'autre est le groupe recherché.

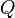
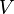
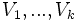
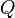
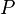
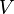
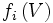
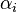
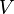
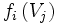
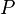
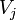
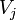
Si l'on prend l'une de ces permutations cela va entraîner une permutation sur les et les quantités rationnellement connues étant les coefficients de , permuter les ne changera pas les quantités rationnellement connues. Alors que faire une permutation en dehors de ce groupe va nous envoyer les sur des , qui sont les racines d'un autre polynômes et donc les coefficients qui nous donnent les quantité connues vont être changés et les quantités connues aussi.

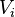
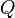
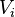
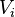
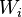
Q.E.D

Extension intermédiaire

Soit les différents ordres sur les racines. Si tous ces ordres se découpent en plusieurs groupes tels que toutes les permutations à l'intérieur de chacun de ces groupes soient les mêmes et si pour deux groupes ils existent une permutation qui les mettent en bijection (on remarquera qu'il s'agit en fait de sous-groupe distingué) alors ils existent une quantité invariante pour chacun de ces groupes et telles que l'on passe de l'une à l'autre par une permutation permettant de passer d'un groupe à l'autre. Alors ces quantités sont racines d'un même polynôme irréductible.

Réciproquement si l'on a une quantité qui s'exprime en les racines, alors chacun des groupes qui fixent l'un de ses conjugués sont tous les mêmes et deux de ces groupes sont en bijection grâce à une seule permutation.

Preuve

Il suffit de prendre encore une fois un polynôme en les racines tel qu'il soit invariant pour toutes les permutations à l'intérieur de l'un de ces groupes et variant pour toutes les autres. Le polynôme va avoir une valeur différente pour chaque groupe et comme l'on passe de l'une à l'autre grâce à toutes les permutations elles sont toutes conjuguées.

À mieux rédiger ce passage car important.