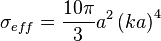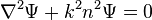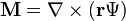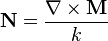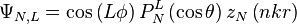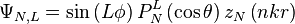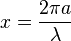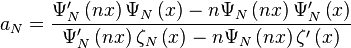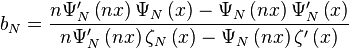Théorie de Mie - Définition

Résolution mathématique

Position du problème

La diffusion de Mie est un problème vectoriel qui implique l'utilisation sous leur forme complète des champs électrique et magnétique.

On se donne une fonction scalaire Ψ qui satisfait l'équation de d'Alembert :

avec n l'indice de réfraction du milieu, k le nombre d'onde et l'opérateur formel nabla. On pose les vecteurs M et N tels que :

avec r le vecteur position. Alors, en coordonnées sphériques, M et N satisfont l'équation de d'Alembert.

La résolution de la diffusion de Mie pour Ψ donne accès aux deux champs vectoriels, desquels on déduit l'onde diffusée.

Résolution et conditions limites

Représentation de la diffusion Mie pour une particule sphérique de 2 µm de rayon, éclairée par la gauche avec de la lumière rouge (λ = 633 nm).

En coordonnées sphériques, il existe des solutions stationnaires à l'équation d'onde. On les exprime en termes d'harmoniques sphériques. Ces solutions sont engendrées par deux fonctions de la forme :

avec N et L deux paramètres entiers, les polynômes de Legendre, z_N les fonctions de Bessel sphériques, r, θ et ϕ sont les coordonnées sphériques.

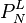
La particule étant de rayon a, la lumière incidente de longueur d'onde λ, on introduit pour simplifier x défini par :

Alors les conditions limites imposent les coefficients de la solution de la diffusion Mie :

avec Ψ et ζ les fonctions de Riccati-Bessel.

La section efficace de la diffusion est donnée par :

.
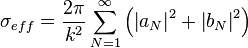