Théorie des collisions - Définition

Survol qualitatif de la théorie

Fondamentalement, la théorie des collisions est basée sur la théorie cinétique des gaz et ne peut donc être appliquée strictement qu'aux gaz parfaits. Son extension à d'autres états de la matière (liquides, solutions) présuppose d'autres approximations. Qualitativement, la théorie considère les molécules des réactifs comme rigides, neutres et sphériques. La base de la théorie est que, pour pouvoir réagir, les molécules de réactifs doivent entrer en collision, d'où son nom. De plus, elle postule que la majorité des collisions ne conduisent pas à une réaction, pour que la transformation soit effective il faut que les deux espèces qui entrent en collision aient :

• une énergie cinétique supérieure à une certaine énergie, appelée l'énergie d'activation, E_a,
• une orientation spatiale convenable (le facteur stérique) l'une par rapport à l'autre.

Ces collisions qui mènent à une réaction sont nommées collisions efficaces. La vitesse de réaction est donc proportionnelle au nombre de collisions efficaces par unités de temps.

La théorie des collisions permet de comprendre l'influence de deux facteurs significatifs qui déterminent la vitesse des réactions en phase gazeuse :

• La concentration: la fréquence des collision est proportionnelle au produit des concentrations des réactifs.
• La température: a deux effets sur la vitesse. D'une part, une augmentation de la température augmente la vitesse moyenne des molécules donc le nombre de collisions, et d'autre part, l'énergie cinétique moyenne des molécules suit la statistique de Maxwell-Boltzmann. La proportion de molécules ayant une énergie supérieure à l'énergie d'activation augmente donc avec la température.

Par contre, la théorie ne permet pas d'estimer directement la valeur du facteur stérique puisqu'elle considère les molécules comme sphériques.

Conclusion

La théorie des collisions à elle seule ne donne pas une interprétation claire de l'énergie d'activation, pas plus qu'un moyen de la calculer en théorie. En revanche, en dépit de sa simplicité, elle fournit une base pour pouvoir définir un comportement cinétique "typique" des molécules, permettant ainsi de s'occuper de cas plus particuliers.

Validité de la théorie et facteur stérique

Lorsqu'une théorie est formulée, sa validité doit être vérifiée. C'est-à-dire qu'il faut comparer ses prédictions avec les résultats observés expérimentalement.

On peut identifier le produit Zρ au coefficient de vitesse k(T) d'une loi de vitesse du second ordre ( ). Selon la théorie des collisions on a donc : .

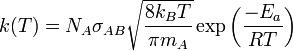
Cette expression est similaire à la loi d'Arrhenius et donne la première interprétation théorique de l'équation d'Arrhenius d'un point de vue moléculaire. La dépendance du facteur pré-exponentiel A avec la température est si faible comparée à celle du facteur exponentiel qu'il ne peut être mis en évidence expérimentalement. C'est-à-dire qu'"on ne peut pas établir expérimentalement, par le biais d'études sur les températures ou sur les coefficients de vitesse, la dépendance T^½ du facteur pré-exponentiel."

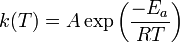
Facteur stérique

Si l'on compare les valeurs des coefficients de vitesse calculés par la théorie des collisions avec les valeurs des coefficients de vitesse obtenus expérimentalement, on constate que la théorie échoue à les estimer correctement, et qu'elle échoue d'autant plus que les molécules sont complexes. D'une part, les valeurs obtenues pour une réaction donnée sont beaucoup trop élevées (parfois d'un facteur de plusieurs puissances de 10), d'autre part, les valeurs obtenues pour différentes réactions sont trop proches les unes des autres. En effet, les ordres de grandeurs des vitesses de réactions varient dans des proportions énormes (de 1 à 10⁵), alors que la taille et la masse des molécules ne varient que de 1 à 10²).

La raison à ceci est que les particules sont supposées sphériques et capables de réagir quelle que soit leur orientation l'une par rapport à l'autre(en fait pour une sphère toutes les directions sont équivalentes). Cela n'est pas vrai, car l'orientation des molécules les unes par rapport aux autres n'est pas toujours la bonne. Par exemple, dans le cas de la réaction d'hydrogénation de l'éthylène, la molécule de di-hydrogène H₂ doit approcher la zone de liaison entre les atomes d'éthylène, et seulement une faible proportion de toutes les collisions qui se produisent sont effectivement dans ce cas.

Un nouveau concept doit ainsi être introduit, celui de facteur stérique, ρ. Il est défini comme le rapport entre la valeur expérimentale et la valeur prédite (ou le rapport entre le facteur pré-exponentiel et la fréquence de collision), et vaut la plupart du temps moins que 1. Ce facteur est parfois appelé facteur de probabilité ou facteur d'Hinshelwood du nom du physico-chimiste anglais Sir Cyril Norman Hinshelwood qui l'a introduit dans les années 1935.

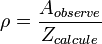
Généralement, plus les molécules réactives sont complexes, plus le facteur stérique est faible. Néanmoins, certaines réactions montrent des facteurs stériques valant plus de l'unité, comme les réactions de Harpoon, qui impliquent des échanges d'électrons et qui produisent des ions. La déviation par rapport à l'unité du facteur stérique peut avoir différentes causes : les molécules ne sont pas sphériques, donc il existe différentes géométries envisageables; seulement une partie de l'énergie cinétique des molécules est fournie au bon endroit; la présence de solvant peut être un problème dans le cas des solutions... Malheureusement, le facteur stérique, de par sa définition, ne peut être calculé théoriquement. L'intérêt pratique d'un point de vue expérimental de la théorie des collisions est ainsi grandement diminuée.

La théorie des collisions peut être appliquée aux réactions en solution; dans ce cas l'effet de cage a une incidence sur les molécules réactives et plusieurs collisions peuvent se produire au cours d'un seul choc, ce qui amène le facteur pré-exponentiel à avoir une valeur plus importante que prévue. Les valeurs ρ plus grandes que l'unité peuvent être attribuées à des contributions entropiques favorables.