Théorie des collisions - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
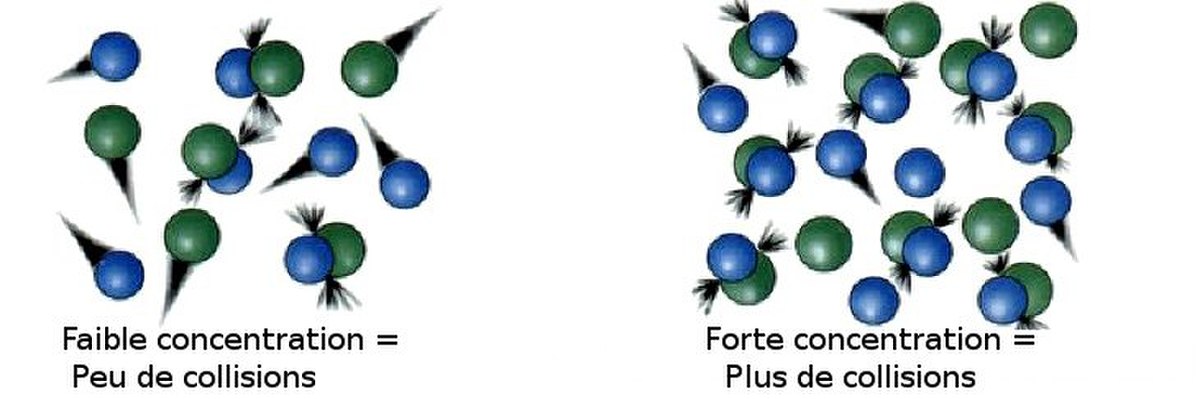
La Théorie des collisions est une théorie qui explique qualitativement comment se produisent les réactions chimiques élémentaires en phase gazeuse et qui rend compte de la dépendance de leur vitesse avec la concentration . Elle suppose que pour qu'une réaction se produise, les molécules des réactifs doivent entrer en collision. Seulement une fraction des collisions se traduisent par la transformation effective des réactifs en produits (on les appelle collisions efficaces). Cela est dû au fait que seulement une partie des molécules ont une énergie suffisamment et la bonne orientation au moment de l'impact pour rompre les liaisons existantes et en former de nouvelles. L'énergie minimale pour que la réaction puisse se produire est appelée énergie d'activation. La théorie des collisions est ainsi très intimement liée à la théorie cinétique des gaz elle constitue un des fondements théoriques de la cinétique chimique
Coefficient de vitesse
Le coefficient de vitesse d'une réaction bimoléculaire en phase gazeuse, est donné selon la théorie par :
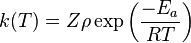
- Z est la fréquence de collision
-

- Ea est l'énergie d'activation du complexe activé selon Eyring
- T est la température
- R est la constante universelle des gaz parfaits
Et la fréquence de collision est donnée par :
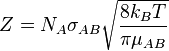
- NA est le nombre d'Avogadro
- σAB est la section efficace de la réaction
- kB est la constante de Boltzmann
- μAB est la masse réduite des réactifs
Aspect quantitatif de la théorie
Développement
La théorie des collisions ne peut être appliquée quantitativement qu'aux réactions bimoléculaires en phase gazeuse, du type
-
- A + B → C
Les molécules sont considérées comme des sphères rigides. Une molécule du réactif A et une molécule du réactif B entreront en collision lorsque la distance entre leurs centres devient inférieure à la somme de leurs rayons respectifs. La surface autour d'une molécule de A dans laquelle il peut se produire une collision avec une molécule de B approchante est appelée la section efficace (σAB) de la réaction. Elle est, en principe, la surface correspondant au cercle dont le rayon (rAB) est la somme des rayons des deux molécules réactives. L'hypothèse de sphéricité de la molécule permet de dire qu'une molécule en mouvement couvrira un volume de
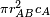
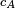
La théorie cinétique des gaz conduit à l'expression de la vitesse moyenne d'une molécule :
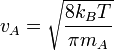
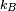
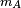
La solution du problème à deux corps nous dit que deux corps différents en mouvement peuvent être assimilés à un seul corps possédant la masse réduite de ces deux corps et se déplaçant à la vitesse du centre de masse. Ainsi, dans l'expression précédente on doit utiliser la masse réduite μAB au lieu de mA.
Donc, la fréquence de collision de toutes les molécules de A avec toutes les molécules de B, est donnée par :
![N_A \sigma_{AB} \sqrt \frac{8 k_B T}{\pi \mu_{AB}}[A][B] =N_A r^{2}_{AB} \sqrt \frac{8 \pi k_B T}{ \mu_{AB}}[A][B] = Z [A][B]](https://static.techno-science.net/illustration/Definitions/autres/0/0865d22fd6fe756ba482a779d824c31d_c5493bfd1c3f318cef1aa89481d73200.png)
De la statistique de Maxwell-Boltzmann il peut être déduit que la fraction des collisions ayant une énergie supérieure à l'énergie d'activation est
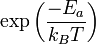
![r = Z \rho [A][B] \exp \left( \frac{-E_{a}}{RT} \right)](https://static.techno-science.net/illustration/Definitions/autres/b/bb4fd45453eb7893a06f20e52fcf1e9e_3d5e2914b69ea705d7e96d2c81988042.png)
![r = Z \rho \exp \left( \frac{-E_{a}}{RT} \right) [A][B]](https://static.techno-science.net/illustration/Definitions/autres/d/da51653ea4ea5f9e5f5e1b94b47866e3_11fb1f68dab941f9239481ca5ae15930.png)
Où
-
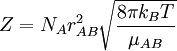
-

- Ea est l'énergie d'activation de la réaction
- T est la température
- R est la constante des gaz parfaits
Le produit Zρ est équivalent au facteur pré-exponentiel de la loi d'Arrhenius.