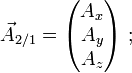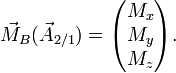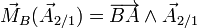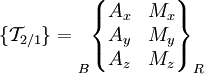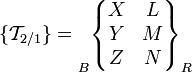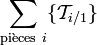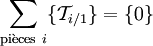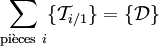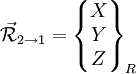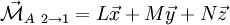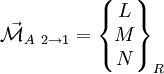Torseur statique - Définition

Introduction

Le torseur statique, ou torseur d'action, est largement utilisé pour modéliser les actions mécaniques lorsqu'on doit résoudre un problème de mécanique tridimensionnelle en utilisant le principe fondamental de la statique. Le torseur statique est également utilisé en résistance des matériaux. On utilisait autrefois le terme de dyname.

Approche « empirique »

Le torseur est un objet mathématique abstrait, dont l'étude théorique peut être rebutante pour des personnes ne l'utilisant que comme un outil. Il peut cependant être utile de le voir comme une manière d'organiser les informations.

En effet, la résolution des problèmes de statique, de dynamique et de résistance des matériaux fait intervenir les forces et les moments :

Principe fondamental de la statique (PFS)

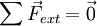
et

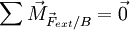
où B est un point quelconque ;

Principe fondamental de la dynamique (PFD)

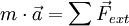
et

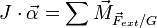
où G est le centre d'inertie de l'objet.

Considérons deux pièces notées 1 et 2 en contact au point A. Notons la force de contact de la pièce 2 sur la pièce 1 en ce point A.

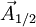
Pour les problèmes hors d'un plan, les vecteurs-force ont trois composantes, et il faut utiliser des vecteurs-moment à trois composantes :

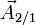
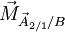
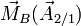
Le moment en B de la force , noté ou , s'écrit :

où désigne le produit vectoriel.

Notons que l'action de contact entre 1 et 2 peut aussi comporter un moment en A (cas par exemple d'un tournevis qui exerce à la fois une force de pression et un couple de torsion à la vis). On a alors

.

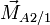
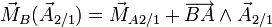
En notant R la résultante, on peut retenir le moyen mnémotechnique BABAR :

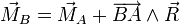
On peut regrouper les composantes des deux vecteurs dans un même objet que l'on appelle « torseur », et noté :

où R désigne le repère dans lequel sont écrits les composantes des vecteurs. Les composantes du torseur sont en général notés X, Y, Z, L, M, N :

La résultante des actions extérieures sur la pièce 1 s'écrit

Le PFS s'écrit alors :

et le PFD s'écrit

où est le torseur dynamique.

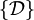
On utilise les termes de :

• torseur d'action pour désigner le torseur statique décrivant l'action mécanique d'une pièce sur une autre, voir Liaison mécanique#Statique et dynamique ;
• torseur de cohésion ou torseur des efforts intérieurs pour désigner le torseur statique décrivant un effort interne à une pièce (résistance des matériaux), voir Principe de la coupure.

Composantes dans un repère donné

Résultante du torseur

La résultante du torseur du torseur est un vecteur qui peut être projeté suivant les trois axes du repère R associé. On peut donc écrire :

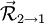
La résultante du torseur est invariable quel que soit le point d'écriture du torseur.

L'unité internationale utilisée pour quantifier une force est le newton (N).

Moment du torseur

Le moment du torseur est un vecteur qui possède trois composantes notées L, M, N. Le moment du torseur s'écrit alors

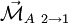
où , et sont les vecteurs formant la base orthonormée du repère R.

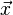
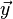
Le moment du torseur peut également être noté

Lorsqu'on veut connaître les composantes d'un moment en un point B connaissant entièrement celles-ci en un point A et connaissant le vecteur déplacement , on utilise la relation de Varignon :

.

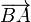
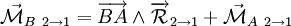
L'unité internationale utilisée pour quantifier un couple est le newton mètre (N⋅m).