Transformation conforme - Définition
La liste des auteurs de cet article est disponible ici.
Applications pratiques
Mécanique des fluides
Au début de l'aérodynamique la transformation conforme a fourni, sous des hypothèses restrictives, une méthode élégante de calcul de l'écoulement bi-dimensionnel autour d'un profil d'aile et de sa portance. Certaines transformations bien choisies permettent en effet de transformer un cercle en une courbe ressemblant à un profil d'aile et en déduire la portance d'une aile de grand allongement.
La première application de cette technique correspond à ce qu'on appelle la transformation de Joukovsky :
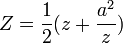
Cette équation simple conduit à un profil qui présente divers inconvénients mais des transformations plus pertinentes ont été utilisées systématiquement.
Cartographie
Certaines projections cartographiques sont conformes. Citons par exemple la projection stéréographique (plane), la projection de Mercator et sa généralisation (cylindriques), et la projection de Lambert (conique).
Cas de la dimension n ≥ 3
Les transformations conformes sont les difféomorphismes dont la jacobienne est une similitude ; Liouville a démontré que, contrairement au cas du plan, les seules transformations conformes en dimension n ≥ 3 sont les produits d'inversions et de similitudes, c'est-à-dire les transformations conservant l'ensemble des hypersphères et des hyperplans.

















































