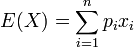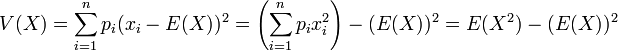Variables aléatoires élémentaires - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
La notion de variable aléatoire réelle est utilisée dès que le résultat d’une expérience aléatoire est quantifiable. Elle est née de considération sur les jeux où à chaque jeu pouvait être associé un gain (= somme empochée - mise). La question était de savoir comment répartir de façon juste les mises en cas d’arrêt forcé en cours de partie. Blaise Pascal contribua grandement à la fonder.
De manière informelle, une variable aléatoire réelle est une variable numérique qui dépend d'une expérience soumise au hasard. C'est le cas des gains d'un joueur qui dépendent du résultat d'un tirage de loterie ou bien de la somme des faces supérieures de deux dés qui dépend du résultat du lancé des deux dés. À chaque résultat de l'expérience soumise au hasard est associé un nombre (gain ou somme des chiffres). Cette relation entre l'ensemble des résultats possibles d'une expérience aléatoire, que l'on appelle univers des possibles, et un ensemble de nombres est à l'origine de la définition formelle de la variable aléatoire.
Formellement, une variable aléatoire réelle est une application X d’un univers Ω muni d’une probabilité p vers R. Cette application crée un nouvel univers X(Ω) de réels sur lequel on peut construire une probabilité issue de p. Cette probabilité s’appelle loi de probabilité de X. Il arrive souvent que l’on oublie l’univers Ω pour ne s’intéresser qu’à l’univers X(Ω).
Cas des variables aléatoires définies sur un univers Ω fini.
Si l’univers Ω est fini, alors l’univers X(Ω) est fini. X(Ω) = {x1, x2, ..., xn}.
Loi de probabilité
Attention : l’approche fréquentiste utilisée dans cette section ne résume pas à elle seule la notion de probabilité. Elle ne fait qu’en fournir un exemple. Nombre de probabilités sont associées à des événements où aucune notion de fréquence n’intervient.
La loi de probabilité peut se construire de la manière suivante : pX(xi) = p(X = xi). = pi
Exemple: En lançant deux dés, on crée un univers Ω de 36 éléments formé de couples d’entiers de 1 à 6. Sur cet univers, on définit une équiprobabilité (les lancers des 2 dés étant deux expériences indépendantes). Si l’on ne s’intéresse qu’à la somme des deux dés, il faut créer une variable aléatoire X qui, à chaque couple, associe leur somme.
L’univers X(Ω) est donc {2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12}. Cet univers contient 11 éléments, mais il n’est pas adéquat d’y définir une équiprobabilité.
- pX(7) = p(X = 7) = p({(1 , 6)}) + p({(2, 5)}) + p({(3 , 4)}) + p({(4 , 3)}) + p({(5 , 2)}) + p({(6 , 1)}) = 6/36 = 1/6
- pX(2) = p(X = 2) = p({1 , 1}) = 1/36
On peut ainsi créer une loi de probabilité sur X(Ω)
| xi | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| pi | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Espérance, variance et écart type
La présentation de la loi de probabilité sous forme d’un tableau ressemblant au tableau des fréquences d’une série statistique quantitative discrète et la loi des grands nombres qui stipule que les deux tableaux coïncident si on renouvelle un grand nombre de fois l’expérience, pousse à définir aussi pour X la moyenne, la variance et l’écart type.
La moyenne de la série statistique sera appelée espérance dans le cas d’une variable aléatoire. Ce terme provient sans doute de l'utilité des premières variables aléatoires dans les calculs statistiques sur les gains des jeux de hasard. L’espérance du gain correspond alors à la moyenne des gains au cours de nombreuses parties.
La variance s’écrit alors, par analogie avec la formule de la variance avec fréquences:
L’écart type reste toujours la racine carrée de la variance :
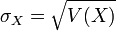
Fonction de répartition
La fonction de répartition d'une variable aléatoire X est la fonction F définie sur R par F(x) = p(X ≤ x).
Dans le cas d’une variable discrète, c’est une fonction en escalier. En effet :
- si x < x1 alors F(x) = 0.
- si
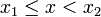
- si
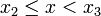
- ...
- si
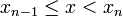
- si
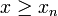
Lois célèbres
Outre l’équiprobabilité, on peut rencontrer aussi