Variété abélienne - Définition
La liste des auteurs de cet article est disponible ici.
Module de Tate
Nous avons vu que sur ℂ, A est un quotient (comme variété analytique) de ℂn par un réseau Λ. Sur un corps k quelconque, il existe un équivalent du réseau Λ, c'est le module de Tate.
Définition Soit l un nombre premier distinct de l'exposant caractéristique de k. On a un système projectif
![(A(\bar{k})[l^n])_n](https://static.techno-science.net/illustration/Definitions/autres/2/2ca39c3e238bda2aa9bce4d6ef40f300_354b5076d42a372aa69c920471094604.png)
![(A(\bar{k})[l^n])_n](https://static.techno-science.net/illustration/Definitions/autres/2/2ca39c3e238bda2aa9bce4d6ef40f300_354b5076d42a372aa69c920471094604.png)
Le module de Tate est naturellement un module sur l'anneau ℤl des entiers l-adiques.
Proposition Tl(A) est isomorphe à ℤ
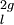
Le groupe de Galois absolu Gal(ks / k) agit naturellement sur Tl(A) à travers son action sur les points de torsion
![A(\bar{k})[l^n]](https://static.techno-science.net/illustration/Definitions/autres/b/b590f3098e6518ab60db2c075b3164a2_63dd69e5a28e85a73e1b5173b3ab1ab4.png)
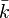
Anneaux d'endomorphismes
Soit A une variété abélienne sur k de dimension g. On note End(A) l'ensemble des endomorphismes de A.
Théorème L'ensemble End(A) est naturellement un anneau. Comme module sur ℤ, il est libre de rang au plus 4g.
La structure de l'anneau End(A) est plus simple lorsqu'on permet d'inverser les entiers naturels. On note End^0(A) le produit tensoriel sur ℤ de End(A) par le corps des rationnels Q.
Théorème Si A est isogène au produit
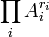
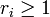
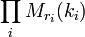
Polarisation
Lorsque le corps de base k est algébriquement clos, une polarisation sur A est une isogénie
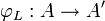
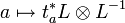
Sur un corps de base quelconque, une polarisation sur A est une isogénie
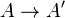
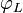
Une variété abélienne munie d'une polarisation est appelée une variété abélienne polarisée. Le degré de la polarisation est simplement le degré de l'isogénie. Une polarisation principale est une polarisation de degré 1, donc un isomorphe. Une variété abélienne principalement polarisée est une variété abélienne munie d'une polarisation principale. Toute jacobienne de courbe est principalement polarisée (donc isomorphe à sa duale) avec la polarisation définie par le diviseur thêta.
Variété abélienne duale
- Définition Soit A une variété abélienne sur un corps k. On montre que le foncteur de Picard relatif PicA / k est représentable par un schéma en groupe lisse sur k. Sa composante neutre (composante connexe de l'élément neutre)
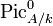
- Description Si
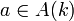
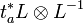
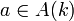
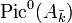
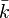
- Fibré de Poincaré Il existe un faisceau inversible P sur
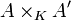
-
- La restriction
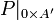
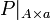
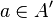
- La restriction
-
- Le faisceau P est universel dans le sens suivant: pour tout schéma T sur k, et pour tout faisceau inversible L sur
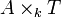
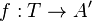
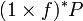
- Le faisceau P est universel dans le sens suivant: pour tout schéma T sur k, et pour tout faisceau inversible L sur
- Réflexivité La duale de la duale (A')' est isomorphe à A.

















































