Variété différentielle - Définition

Applications différentiables

Définition

La différentiabilité d'une fonction f entre deux variétés différentielles M et N se définit en procédant à la lecture de f dans des cartes locales au voisinage de chaque point.

Formellement, on considère deux variétés M et N de classe C^k et un entier j inférieur à k. Une application est dite de classe C^j quand, pour tout point m de M, on peut trouver une carte locale (U,φ) de M centrée en m et une carte locale (V,ψ) de N centrée en n=f(m) telles que

est bien définie et est de classe C^j de φ(U) dans ψ(V).

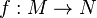
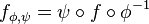
Si on considère de nouvelles cartes locales, la régularité des applications de changement de cartes assure que les fonctions f_φ',ψ' correspondantes seront régulières, ce qui montre la cohérence de la définition.

Il est un peu plus délicat de définir la notion de différentielle d'une application différentiable, puisque cela demande d'introduire au préalable les vecteurs tangents. Cependant, le rang de la différentielle de f_φ,ψ au point m ne dépend pas des cartes choisies. On parle notamment d'immersion si ce rang est égal en tout point à la dimension de M, de submersion s'il est égal en tout point à la dimension de N.

Variétés isomorphes

La composée d'applications de classe C^j entre deux variétés, quand elle existe, est de classe C^j. Les variétés différentielles de classe C^k forment une catégorie dont les morphismes sont les applications de classe C^k.

Deux variétés différentielles M et N de classe C^k sont isomorphes lorsqu'il existe un C^k-difféomorphisme de M dans N (c'est-à-dire une application bijective de classe C^k ainsi que sa réciproque).

Du point de vue du calcul différentiel, il est possible d'identifier deux variétés isomorphes. La géométrie différentielle a pour objet premier l'étude des structures différentielles modulo la relation d'isomorphisme.

Existence et unicité de structures différentielles

Alors que la théorie des variétés différentielles est foncièrement différente de celle des variétés topologiques, le degré de différentiabilité utilisé est sans importance autre que technique. On a en effet le théorème

Soient k₁ ≤ k₂ dans (N\{0})∪{∞, ω} (ω pour analytique). Toute variété de classe C^k₁ est C^k₁-difféomorphe à une variété de classe C^k₂. Si deux variétés de classe C^k₂ sont C^k₁-difféomorphes, alors elles sont C^k₂-difféomorphes.

Ce théorème s'interprète naïvement en disant qu'on peut retirer d'un atlas C^k₁ des cartes qui se recollent mal (dont les applications changement de carte ne sont pas de classe C^k₂). On obtient alors un atlas avec moins de cartes, mais de classe C^k₂. A l'extrême s'il ne reste plus qu'une seule carte dans l'atlas (la variété étant alors homéomorphe à un ouvert de Rⁿ), dans ce cas l'atlas est analytique.

On connaît au contraire des variétés topologiques qui admettent plusieurs structures différentielles non isomorphes. Le premier exemple, découvert en 1956 par John Milnor, est la sphère de dimension 7. Il existe par ailleurs des variétés topologiques qui n'admettent aucune structure différentielle (Michel Kervaire, 1960).

Les questions d'existence et d'unicité ne se posent qu'à partir de la dimension 4, puisqu'une variété topologique de dimension inférieure à 3 possède une unique structure différentielle. La dimension 4 est la première dimension pour laquelle l'existence et l'unicité sont mises en défaut.

Cette dimension joue à plusieurs égards un rôle particulier : on sait ainsi que pour toute valeur de n différente de 4, l'espace possède une unique structure différentiable, alors qu'il existe une infinité non dénombrable de structures non isomorphes sur . En toute dimension autre que 4, une variété topologique compacte possède au plus un nombre fini de structures différentielles non isomorphes. Ces découvertes reposent sur une succession de travaux publiés entre 1982 et 1987. En 1982, Michael Freedman établit la classification des variétés topologiques compactes simplement connexes de dimension 4. L'année suivante, Simon Donaldson montre que les structures différentielles sont soumises à des contraintes beaucoup plus fortes ; il découvre également de nouveaux invariants de la structure différentielle. Ces travaux sont exploités pour montrer l'existence de structures exotiques sur  : Clifford Taubes montre même en 1987 qu'il en existe une infinité non dénombrable.

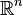
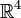
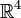
Sous-variétés, plongements

Soit M une variété différentielle et son atlas maximal de classe C^k. Une partie N de M est une sous-variété différentielle de codimension d, si N en est une sous-variété topologique de dimension n-d et si N respecte l'atlas au sens suivant

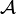
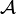
Au voisinage de chaque point x de N, il existe une carte locale pour laquelle .

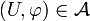
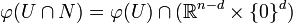
Autrement dit, un point p est dans N ssi les d dernières coordonnées de φ(p) sont nulles. La partie N est alors naturellement munie d'une structure de variété C^k de dimension n-d, induite par celle de M ; à savoir la classe de C^k-équivalence dans N de l'atlas formé par les cartes φ dont les d dernières coordonnées s'annulent sur N.

Ainsi, certaines courbes et surfaces classiques du plan ou de l'espace forment des sous-variétés, mais pas toutes, par exemple à cause de l'existence de points multiples. Si la courbe ou la surface est définie de façon paramétrique, on peut donner des conditions suffisantes sur l'application de paramétrage pour que l'image soit une sous-variété, ce qui conduit à la notion générale de plongement. On peut aussi donner des conditions pour qu'une courbe ou surface définie par une ou des équations soit une sous-variété. L'équivalence locale entre ces différents points de vue est donnée par le théorème des fonctions implicites.

De façon générale, un plongement permet d'inclure une variété dans une autre en respectant la structure différentielle. Une application p d'une variété X dans M est appelée plongement quand p est une immersion et un homéomorphisme sur son image Y=p(X). Dans ce cas, Y est une sous-variété de M. Le théorème de plongement de Whitney montre que toute variété différentielle peut être plongée dans un espace pour un p suffisamment grand, c'est-à-dire que toute variété peut-être vue comme sous-variété d'un tel espace vectoriel.

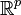
On dispose d'une généralisation de la définition d'une sous-variété par équation. Si est une submersion entre les variétés différentielles M et N, et si n appartient à N, alors l'image réciproque f ^{− 1}(n) est une sous-variété de codimension égale à la dimension de N.

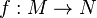
Notamment, les variétés de codimension 1 sont appelées hypersurfaces de M. Elles peuvent être obtenues, localement, comme images réciproques pour des fonctions numériques définies sur M et sans point critique.