Équation de Helmholtz - Définition
L'équation de Helmholtz (d'après le physicien Hermann von Helmholtz) est une équation aux dérivées partielles elliptique qui apparaît lorsque l'on cherche des solutions stationnaires de l'équation de propagation des ondes de d'Alembert, appelées " modes propres ", sur un domaine
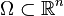
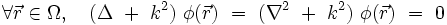
Pour que le problème mathématique soit bien posé, il faut spécifier une condition aux limites sur le bord
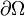
- soit la condition de Dirichlet (le champ scalaire est nul sur le bord),
- soit la condition de Neumann (la dérivée normale du champ scalaire est nulle sur le bord).
Lorsque le domaine Ω est compact, le spectre du Laplacien est discret, et les modes propres forment un ensemble dénombrable infini :
L'équation de Helmholtz se généralise en géométrie non-euclidienne en remplaçant le Laplacien par l'opérateur de Laplace-Beltrami sur une variété riemannienne.

















































