Système duodécimal - Définition
Le système duodécimal est un système de numération de base 12.
En base 12, on utilise les 10 chiffres de 0 à 9, suivis les lettres A et B, respectivement pour 10 et 11. On utilise parfois aussi à la place de ces dernières, respectivement, les lettres α (alpha minuscule) et β (bêta minuscule), ou bien T (de l'anglais ten) et E (de l'anglais eleven), ou encore X (chiffre romain) pour dix.
Il existe deux organismes la Dozenal Society of America et la Dozenal Society of Great Britain qui font la promotion du système duodécimal en affirmant qu'un système en base 12 est meilleur que le système décimal tant d'un point de vue mathématique que pour d'autres cotés pratiques. En effet 2, 3, 4, 6 sont des facteurs de 12, ce qui facilite la mise en fraction. Comparé au facteur 2 et 5 du système décimal, le système duodécimal offre plus de possibilités.
L'utilisation d'un système en base 12 n'est pas courant, pourtant il existe un exemple pratique utilisé dans le langage du Népal. Dans le passé, les romains, malgré le décompte en base 10, utilisaient le système duodécimal pour représenter les fractions.
Historiquement le nombre 12 a été utilisé par de nombreux peuples. Il est reconnu que l'observation des 12 phases de pleine lune dans une année explique l'universalité de ce nombre dans toute les cultures. Des exemples de cet usage sont les 12 mois de l'année, les 12 heures d'une montre, les 12 divisions traditionnelles du temps dans une journée en Chine, les 12 signes du zodiaque de l'astrologie, les 12 signes du zodiaque de l'astrologie chinoise, etc. Dans de nombreux langages européens, tel l'anglais, le français, et l'allemand, l'usage de noms spéciaux pour 11 et 12 plutôt que leur nom représenté par le système décimal (douze, twelve) peut faciliter le comptage en base 12. Il est beaucoup utilisé dans le commerce (douzaine, grosse...).
En ayant l'avantage d'être un diviseur simple dans les fractions peut expliquer pourquoi les Britanniques utilisent 12 pouces dans un pied, 12 onces dans un pound, 12 penny dans un shilling, 12 pièces dans une douzaine, 12 douzaines dans une grosse, 12 grosses dans une grande grosse, etc.
| Duodécimal | Equivalent en décimal |
|---|---|
| 10 : douze (ou une douzaine) | 12 |
| 100 : une grosse | 122 = 144 |
| 1 000 une grande grosse | 123 = 1 728 |
| 10 000 douze grande grosse | 124 = 20 736 |
| 100 000 | 125 = 248 832 |
| 1 000 000 | 126 = 2 985 984 |
| 0,1 | 1/12 |
| 0,01 | 1/144 |
15 une douzaine et cinq 3E trois douzaines et onze XE7 dix grosses onze douzaines et sept 11E0 une grande grosse une grosse onze douzaines (= l'année 2004) 36 X17 trois douzaines et six grandes grosses dix grosses une douzaine et sept
Fractions
Le système duodécimal a l'avantage d'avoir des résultats de fractions très simples :
- 1 / 2 = 0,6
- 1 / 3 = 0,4
- 1 / 4 = 0,3
- 1 / 6 = 0,2
- 1 / 8 = 0,16
- 1 / 9 = 0,14
ou compliqués (X = dix, E = onze) :
- 1 / 5 = 0,2497 2497 avec chiffres périodiques (nombre que l'on peut arrondir à 0,25)
- 1 / 7 = 0,186X35 186X35 avec chiffres périodiques
- 1 / X = 0,1 2497 2497 avec chiffres périodiques (nombre que l'on peut arrondir à 0,125)
Comme expliqué dans les décimales répétitives, chaque fois qu'une fraction est écrite en notation décimale, quel que soit sa base, la fraction peut être exprimée exactement, si et seulement si tous les facteurs premiers du dénominateur sont des nombres premiers de la base adoptée.
Ainsi, en base 10 (= 2 × 5), les fractions dont les dénominateurs sont constitués de multiples de 2 ou 5 sont finies :
-
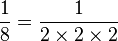
-
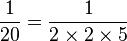
et
-
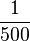
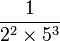
peuvent être exprimées exactement sous forme décimale comme 0,125, 0,05, et 0,005 respectivement. Cependant,
-


donnent les répétitions 0,333... et 0,142857 142857...
Dans le système duodécimal (= 2×2×3),
- 1 / 8 est exact ;
- 1 / 20 et 1 / 500 ont des décimales périodiques parce que leurs dénominateurs incluent 5 dans leur décomposition ;
- 1 / 3 est exact ;
- 1 / 7 est périodique, comme en base 10.
On peut argumenter que les facteurs de 3 sont plus facilement rencontrés dans la vraie vie que ceux de 5 lors des divisions. Mais en pratique la gêne occasionnée par la périodicité des fractions est moins courante lorsque le système duodécimal est utilisé. Cela est particulièrement vrai dans les calculs financiers, lorsque les 12 mois de l'année entrent en ligne de compte dans les calculs.

















































