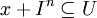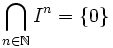Anneau topologique - Définition
En mathématiques, un anneau topologique est un anneau (R,+, ×) muni d'une topologie telle que :
-
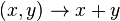
-
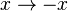
- (
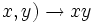
où R 2 est muni de la topologie produit.
Exemples
L'ensemble des rationnels, des réels, des complexes, des nombres p-adiques sont des anneaux topologiques pour leur topologie classique (distance pour les 3 premiers, distance p-adique pour le dernier). Ce sont même des corps topologiques.
L'ensemble des fonctions continues d'un espace topologique E vers l'ensemble des réels est un anneau topologique pour la topologie de la convergence simple.
Topologie I-adique
Si R est un anneau commutatif et I un idéal de R, alors R est un anneau topologique pour la topologie I-adique définie de la manière suivante: Un sous-ensemble U de R est ouvert si et seulement si , il existe un entier naturel n tel que
Si, de plus,
alors R est un espace séparé ou espace de Hausdorff.
La topologie p-adique sur les entiers relatifs est une topologie I-adique avec I = p
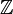
Si R est séparé, on peut induire sur R une distance :
- d(x,y) = 2 − k où k est le premier entier tel que
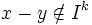
- d(x,y)= 0 si
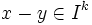
On peut alors parler de suites de Cauchy et rechercher le complété de l'anneau R