Connexité (mathématiques) - Définition
En mathématiques, la notion topologique de connexité formalise le concept d'"être d'un seul tenant ".
Définition
Soit un espace topologique

-

-

- Toute application continue
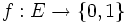
Cette dernière caractérisation est souvent celle qui est la plus commode à utiliser pour démontrer un résultat de connexité.
Dans le cas où ces conditions sont remplies on dit que l'espace

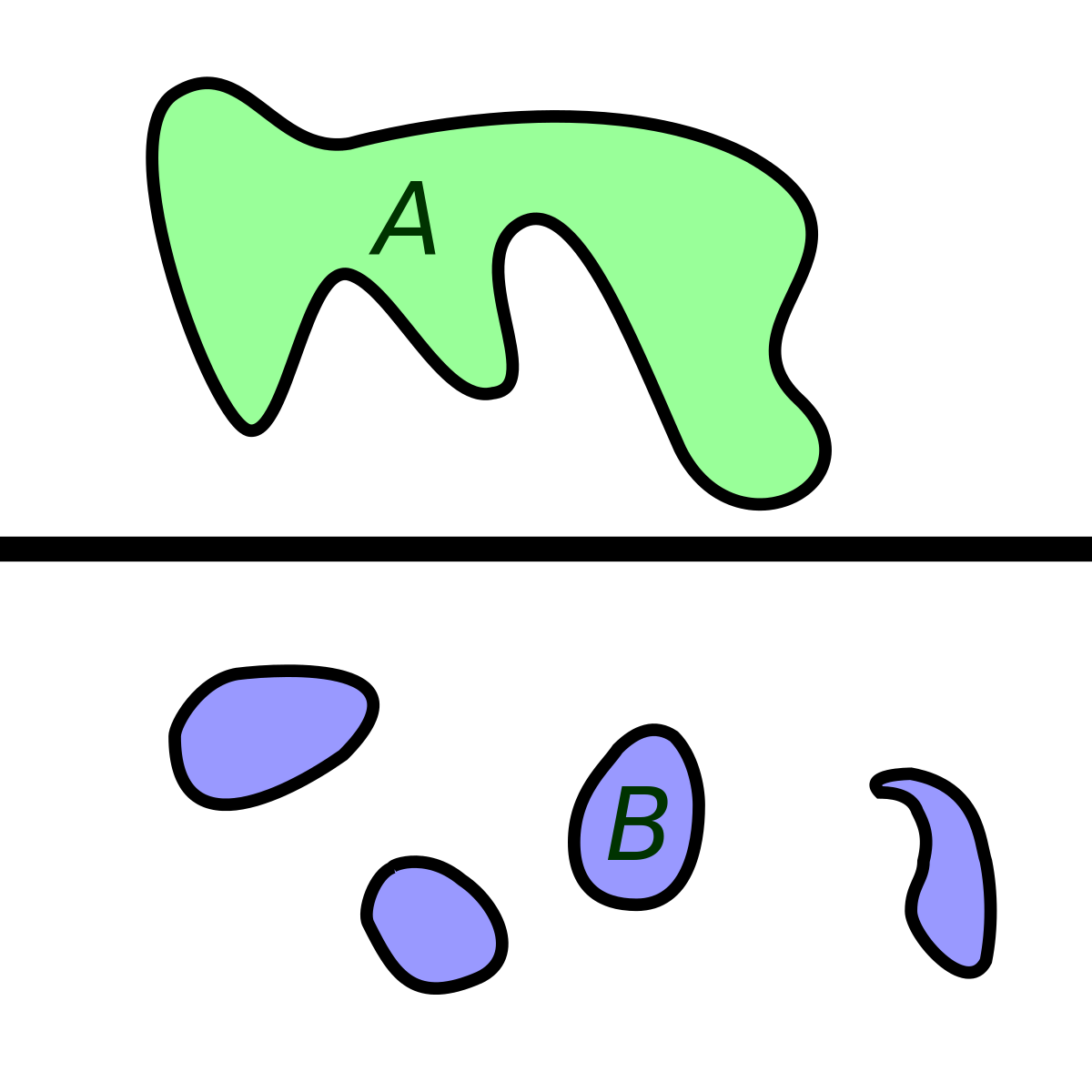
Une partie
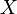

Par exemple un singleton
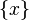
Connexité et nombres réels
- L'ensemble des nombres réels
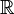
On montre d'abord que tout intervalle fermé borné
![[a,b]\,](https://static.techno-science.net/illustration/Definitions/autres/7/7f3408c72246eece3d5542fc853ce417_5346f07f8b2ea4b5c51d8a4778972123.png)
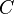
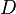
![[a,b]\,](https://static.techno-science.net/illustration/Definitions/autres/7/7f3408c72246eece3d5542fc853ce417_5346f07f8b2ea4b5c51d8a4778972123.png)
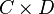
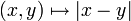
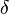
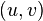
![w=\frac{u+v}{2}\in [a,b]\,](https://static.techno-science.net/illustration/Definitions/autres/a/a2d52fa81df971ea87c28f86c13e26a0_fb81692c79a0d0b8699561e49567fdc1.png)
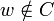
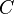
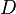
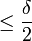
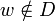
Comme
![\R =\cup_{n\ge 1}[-n,n]\,\!](https://static.techno-science.net/illustration/Definitions/autres/b/bffd68449b3808b3567e843b8e3b3309_3ffb1a2d3231d622640665798a36e973.png)
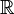
- Les parties connexes de
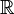
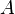
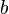
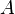
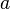
![]-\infty,a[\!](https://static.techno-science.net/illustration/Definitions/autres/a/abaf08b594fbb5acd807f8b2ddf96dd8_3b8913bb181c407d9672f4cc3051c5a0.png)
![]a,+\infty[\!](https://static.techno-science.net/illustration/Definitions/autres/e/ed8178642e0f8ac75bc2dcd8448b1c5d_a49ad7e6fcd9fae417a8cccd6b75d81f.png)
Par exemple
![[0,1] \cup [2,3] \,\!](https://static.techno-science.net/illustration/Definitions/autres/7/73726976a58199c9ac0b0abb04ccb780_6a00707b6d3642f49f7158badf5d1658.png)
Propriétés
Union, intersection, adhérence
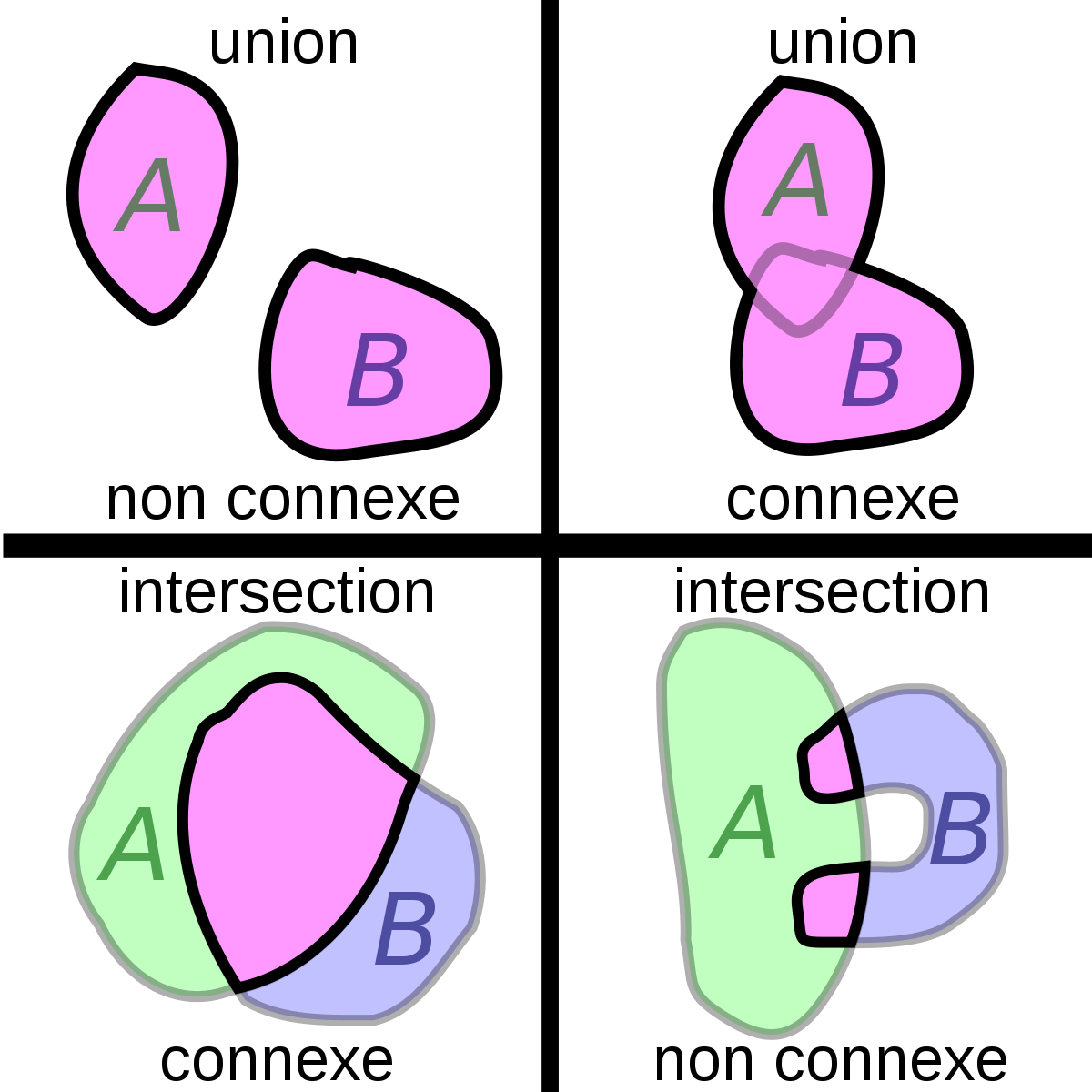
Si
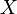
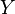

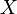
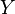
En revanche, l'union des deux parties connexes est connexe si elles ont un point commun. Plus généralement, si
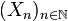
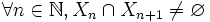
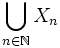
Autre généralisation : la réunion d'une famille quelconque
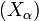

Si
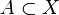
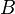
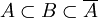
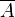
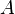
Composantes connexes
Étant donné un point
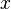

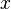
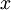
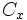
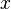

Au minimum, on a
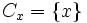
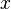
Au maximum, on a
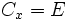

On définit une relation d'équivalence sur

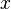
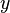
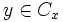
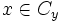
Les classes d'équivalence pour cette relation sont appelées composantes connexes de

Exemples :
-
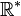
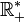
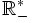
- Dans
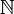
- Dans
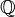
Un espace topologique dont les composantes connexes sont les singletons est dit totalement discontinu.
Connexité et continuité
On sait caractériser les espaces connexes par le fait que toute fonction continue à valeurs dans
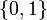
En fait, on peut dire plus généralement que l'image d'un espace connexe par une application continue est toujours connexe. Plus précisément si

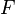
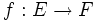
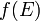
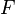
Dans le cas ou
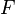
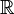

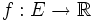
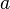
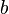

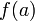
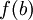
Deux applications fondamentales à l'Analyse
Pour montrer qu'une propriété est vraie pour tous les points d'une partie que l'on sait connexe, on montre que l'ensemble des points qui la satisfait est ouvert et fermé. C'est ce qu'on fait pour le théorème d'unicité global des solutions d'une équation différentielle, et pour le principe du prolongement analytique
Applications à la topologie
La droite

Le même argument montre que le cercle S1 n'est pas homéomorphe à un intervalle.
Cet argument ne s'étend pas aux dimensions supérieures. Si on veut montrer en utilisant les mêmes idées que