Cissoïde - Définition
La cissoïde ou (courbe) cissoïdale de deux courbes (C1) et (C2) par rapport à un point fixe O est le lieu géométrique des points P tels que
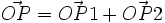
La cissoïde peut aussi être vue comme la courbe médiane de pôle O des courbes C'1 et C'2, images de C1 et C2 par une homothétie de centre O et de rapport 1/2.
Étymologie et histoire
Le terme cissoïde provient du grec kissos lierre et eidos forme. En effet, la cissoïde de Dioclès rappelle la forme d'une feuille de lierre.
Définition mathématique
L'équation polaire de la cissoïde de pôle O des courbes R = f1(θ) et R = f2(θ) est donné par:
R = f1(θ) + f2(θ)
Une cissoïde peut aussi être décrite comme la différence au lieu de la somme de 2 courbes.
Propriétés
- Si (C1) et (C2) sont deux droites parallèles, la cissoïdale est aussi une droite parallèle.
- Si (C1) et (C2) sont deux droites sécantes, la cissoïdale est une hyperbole passant par O, d'asymptotes C1 et C2.
- Si (C2) est un cercle et que le point fixe O est le centre de ce cercle, la cissoïdale est une conchoïde de la courbe (C1).
- Si (C1) est une conique, (C2) est une droite, et que le point fixe O est sur la conique, on obtient une cissoïde de Zahradnik.
- Si (C1) et (C2) sont des cercles et le point fixe O est sur l'un des cercles, on obtient une quartique bicirculaire rationnelle.
- Si (C1) et (C2) sont des cercles et le point fixe O est le milieu des centres, on obtient une courbe de Booth, dont la lemniscate de Bernoulli est un cas particulier.

















































