Foyer (mathématiques) - Définition
On désigne généralement par foyer un ou plusieurs points caractéristiques associés à une figure remarquable de géométrie.
Cas des coniques
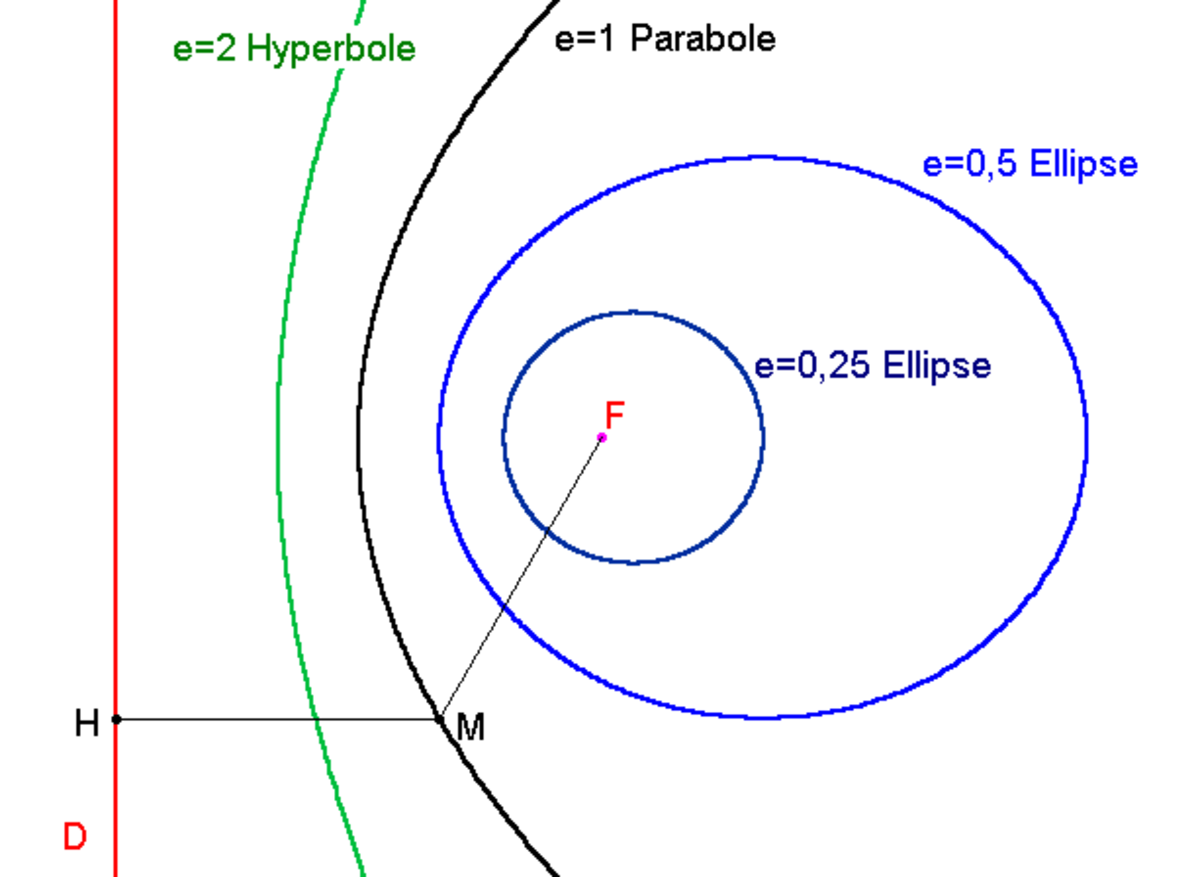
La définition monofocale d'une conique utilise conjointement un foyer F et une droite D appelée directrice associée. La conique apparaît comme ensemble des points M du plan tels que
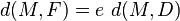
- Les points de la parabole sont donc caractérisés par le propriété MF=MH sur le schéma ci-contre, H désignant le projeté orthogonal de M sur D.
- Plus la valeur e est voisine de 0, plus la conique ressemble à un cercle. Certains estiment que le centre du cercle est son foyer et que la directrice est rejetée à l'infini.
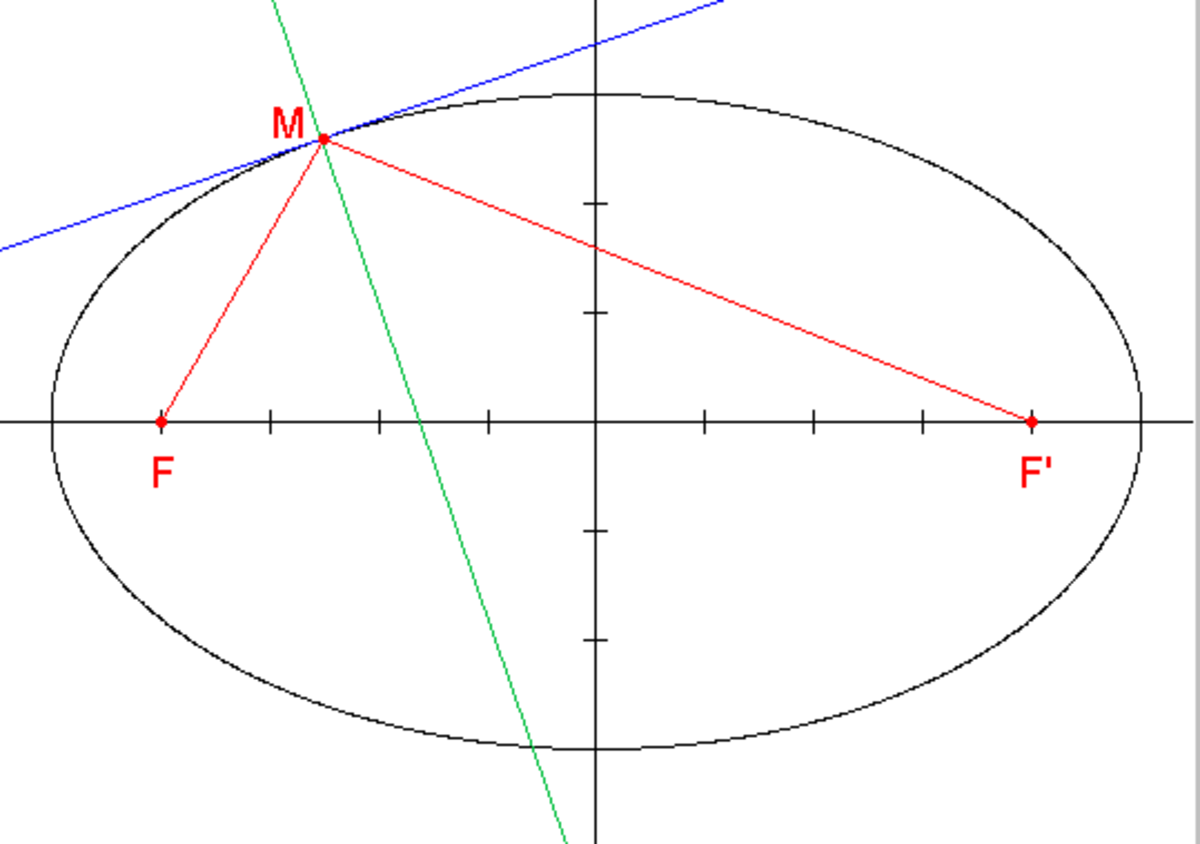
Si la parabole ne possède qu'un foyer, l'ellipse et l'hyperbole en possèdent chacune deux, permettant une définition bifocale de ces courbes. Dans le cas de l'ellipse, la somme des distances du points M aux deux foyers est une constante ; dans le cas de l'hyperbole, c'est la valeur absolue de la différence.
Autres courbes planes
D'autres courbes planes se voient également attribuer des foyers, notamment si leurs points possèdent des propriétés liées aux distances à ces foyers. On peut citer le cas de la lemniscate de Bernoulli, des ovales de Cassini, de certaines cubiques comme la strophoïde ...