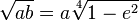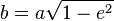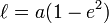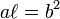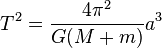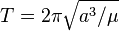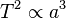Grand axe - Définition
En géométrie, le grand axe d'une ellipse est un paramètre utilisé pour décrire la dimension de cette conique. Le demi-grand axe est la moitié du grand axe.
Définition
Le grand axe d'une ellipse est son plus grand diamètre, un segment qui traverse à la fois le centre et les deux foyers de l'ellipse et la rejoint en ses deux points les plus opposés. Le demi-grand axe correspond à la moitié du grand axe et joint le centre et un bord de l'ellispe à travers l'un des foyers.
De façon similaire, le segment perpendiculaire au grand axe, passant par le centre et rejoignant l'ellipse est son petit axe. Les axes sont les équivalents elliptiques des diamètres d'un cercle, tandis que les demis-axes en sont les analogues des rayons.
La longueur du demi-grand axe a et celle du demi-petit axe b sont liés par l'excentricité e et le paramètre
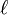
Astronomie
Période orbitale
En astronomie, le demi-grand axe est un élément orbital important, permettant de définir partiellement une orbite. De façon générale, dans le cadre d'un problème à deux corps, la période orbitale d'un corps de masse m orbitant autour d'un autre corps de masse M est :
où :
- a est la longueur du demi-grand axe
- G est la constante gravitationnelle.
Si l'un des corps est suffisamment petit pour que sa masse soit négligée par rapport à l'autre :
où μ est le paramètre gravitationnel standard.
De ce cas, pour toutes les orbites de même demi-grand axe, la période est la même quelle que soit l'excentricité.
On obtient donc la proportionalité suivante :
ce qui correspond à la troisième loi de Kepler.
Distance moyenne
Le demi-grand axe ne correspond pas forcément à la distance moyenne entre les deux corps en orbite, car cette distance dépend du procédé utilisé :
- En calculant la moyenne de la distance sur l'anomalie excentrique, on trouve effectivement le demi-grand axe.
- La moyenne sur l'anomalie vraie donne le demi-petit axe.
- Moyenner sur l'anomalie moyenne conduit à la valeur
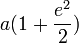
Par ailleurs, le rayon moyen de l'ellipse, mesurée par rapport à son centre, est