Arrangement - Définition
Voir aussi : Arrangement (musique)
En mathématiques, lorsque nous choisissons k objets parmi n objets discernables et que l’ordre dans lequel les objets sont sélectionnés revêt une importance, nous pouvons les représenter par un k-uplet d'éléments distincts.
Exemple : A un examen, cinq candidats tirent les uns après les autres un sujet dans une urne contenant des questions toutes différentes. Le premier tirage se fera sur un ensemble de 50 questions possibles. A chaque tirage suivant, la question qui vient d'être tirée est enlevée de l'urne. Ainsi, s'il on faisait passer 5 élèves, le tirage se ferait sur 50, puis sur 49, et ainsi de suite jusqu'à 46 qui représente l'ensemble des questions restantes dans l'urne pour le dernier tirage. L'arrangement va consister a additioner à chaque modification de cet ensemble de départ la nouvelle probabilité de piocher une question donnée. La solution pour cet exemple est donc un arrangement de 5 (k) à 50 (n). Si on remettait la question tirée de nouveau dans l'urne à chaque tirage, il s'agirait alors d'une combinaison.
Définition :
Soient E un ensemble fini de cardinal n et k un entier naturel. Un k-arrangement sans répétition de E est une application injective de {1, 2, ..., k} dans E.
Autre définition :
Soient E un ensemble fini de cardinal n et k un entier naturel. Un k-arrangement de E (ou k-arrangement sans répétition de E, ou encore arrangement sans répétition de n éléments pris k à k) est un k-uplet (a1, a2, ..., ak) d'éléments de E tel que ai≠aj qqsoit i, j € [1,k] avec i≠j,. Un tel k-uplet est aussi appelé k-liste distincte d'éléments de E.
Théorème :
Soient E et F deux ensembles finis de cardinaux respectifs n et k. L’ensemble
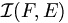
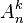
Démonstration :
- Si k > n, alors il n'existe aucune injection de F dans E et donc
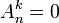
- Si k < n, alors démontrons l'égalité par récurrence sur l'entier k.
- Si k = 1 alors F est un singleton et toute application de F dans E est injective donc
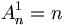
- Supposons l'égalité vérifiée pour tout ensemble F de cardinal k - 1 (2 ≤ k ≤ n) et démontrons la au rang k :
Soit F un ensemble de cardinal k, et x un élément de F. Posons G=F\{x}. Nous avons card(G)=k-1.
Considérons la relation qui relie deux injections de F dans E quand elles ont même restriction à G. Les classes d'équivalence partitionnent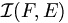
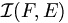
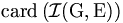
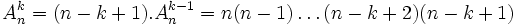
- Si k = 1 alors F est un singleton et toute application de F dans E est injective donc
- Si k=0, nous poserons par convention pour tout entier naturel n
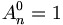
Démonstration (élémentaire):
Si 1 ≤ k ≤ n alors supposons que F={x1, x2, ..., xk}. Pour construire une application injective de F dans E, nous devons
- choisir l'image de x1 et il y a n images possibles,
- choisir l'image de x2 et il reste n-1 images possibles,
- ...
- choisir l'image de xk, il reste dans l'ensemble E n - (k-1) éléments non atteints donc n - (k-1) images possibles.
Au total, nous avons construit n.(n-1).....(n - k + 1) applications injectives différentes.
Corollaire :
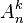
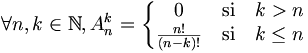
Démonstration :
Supposons F={x1, x2, ..., xk}. Une injection f de F dans E s'identifie au k-uplet d'éléments distincts (f(x1), f(x2), ..., f(xk)). Il y a donc une bijection entre l'ensemble des applications injectives de F dans E et l'ensemble des k-uplets d'éléments distincts de E.
Remarque :
Construire un arrangement revient à placer les uns après les autres, k objets discernables pris parmi n, dans k cases numérotées et donc une permutation de n éléments est un n-arrangement de n éléments. La notion d'arrangement généralise donc celle de permutation.
Voyez aussi
- combinatoire
- arrangement avec répétition
- combinaison
- combinaison avec répétition
- Permutation
- Permutation avec répétition

















































