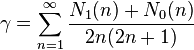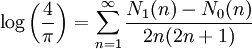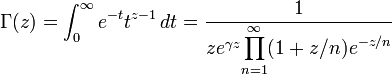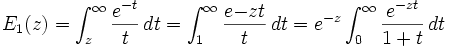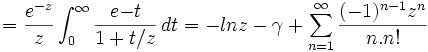Constante d'Euler-Mascheroni - Définition
En mathématiques, la constante d'Euler-Mascheroni est une constante mathématique, utilisée principalement en théorie des nombres, définie comme la limite de la différence entre la série harmonique et le logarithme naturel.
Définition
La constante d'Euler-Mascheroni γ est définie comme étant :
-
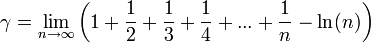
ou, de façon condensée :
-
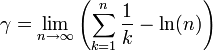
La série harmonique diverge, tout comme la suite de terme général ln(n) ; l'existence de cette constante indique que les deux expressions sont asymptotiquement liées.
Propriétés
Propriétés générales
On ignore toujours si la constante d'Euler-Mascheroni est ou non un nombre rationnel. Cependant, l'analyse en fraction continue de la constante indique que si elle est rationnelle, son dénominateur possède plus de 10242080 chiffres décimaux.
Autres formulations
La constante peut être définie sous la forme explicite d'une série (telle qu'elle fut d'ailleurs introduite par Euler) :
![\gamma = \sum_{k=1}^\infty \left[ \frac{1}{k} - \log \left( 1 + \frac{1}{k} \right) \right].](https://static.techno-science.net/illustrationWebp/Definitions/autres/1/1633fc76bca99f64292d8812df5bc705_e12ac53fd503ddc4ff1b0abdf13b3ad5.png)
Elle est également donnée par plusieurs intégrales :
-
-
-
-
-
-
-
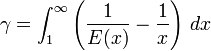
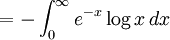
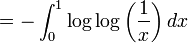
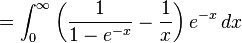
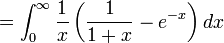
D'autres intégrales mettant en scène γ sont :
-
-
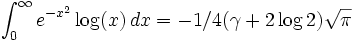
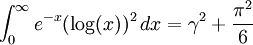
Il est possible d'exprimer γ sous forme d'une intégrale double (avec ici la série équivalente) :
-
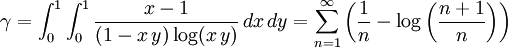
Par ailleurs :
-
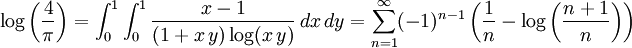
Les deux constantes sont également liées par deux séries :
où N1(n) et N0(n) sont le nombre de 1 et de 0 dans l'écriture de n en base 2.
On trouvera d'autres expressions non classiques de la constante d'Euler dans l'article Mesures secondaires
Relation avec certaines fonctions
La constante d'Euler-Mascheroni possède des liens avec d'autres fonctions particulières :
- Fonction gamma :
-
- Fonction exponentielle intégrale :
-
- Fonction psi :
-
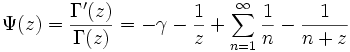
- En particulier,
-
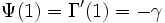
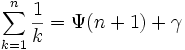
Généralisation
Il est possible de généraliser le sujet en définissant les constantes suivantes :
-
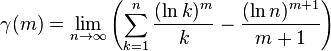
On constate que γ(0) = γ, la constante d'Euler.
Valeur approchée
La 100 premières décimales de la constante d'Euler-Mascheroni sont :
-
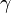
Calcul numérique de γ
Le calcul numérique de γ est un moyen pédagogique simple pour se sensibiliser aux problèmes de propagation d'erreur d'arrondi. En simple précision, pour 100 000 points, en sommant dans l'ordre naturel, on obtient une erreur sur la 4ème décimale, erreur beaucoup plus faible si on fait cette somme dans l'ordre inverse (du plus petit au plus grand), ou si on utilise l'algorithme de Kahan (cf. Somme (algorithmique)). Pour 1 000 000 de points, la divergence atteint la 2e décimale dans le sens naturel, et la 4e décimale dans le sens inverse ; par contre, par la méthode de Kahan, on a atteint les 6 décimales exactes.
