Constante de Meissel-Mertens - Définition
En mathématiques, la constante de Meissel-Mertens (également nommée dans la littérature mathématique constante de Mertens, constante de Kronecker, constante d'Hadamard-de la Vallée-Poussin ou constante des inverses des nombres premiers) est une constante mathématique, utilisée principalement en théorie des nombres, définie comme la limite de la différence entre la série des inverses des nombres premiers et du logarithme naturel du logarithme naturel.
Définition
Soit
-
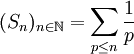
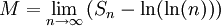
La série des inverses des nombres premiers diverge, tout comme la suite de terme général ln(ln(n)) ; l'existence de cette constante indique que les deux expressions sont asymptotiquement liées :
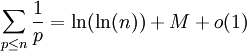
Propriétés
La constante de Meissel-Mertens peut être exprimée en fonction de la constante d'Euler-Mascheroni γ, qui possède une définition similaire impliquant la différence entre la somme de l'inverse de tous les nombres entiers et le logarithme naturel :
-
![M = \gamma + \sum_{p=1}^{\infty} \left[ \ln \left( 1 - \frac{1}{p} \right) + \frac{1}{p} \right]](https://static.techno-science.net/illustration/Definitions/autres/d/d0902200843df2ed9068714f66ebb43c_fb77d3e3a0890c01dd0fdf010a772b20.png)
![M = \gamma + \sum_{p=1}^{\infty} \left[ \ln \left( 1 - \frac{1}{p} \right) + \frac{1}{p} \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d0902200843df2ed9068714f66ebb43c_fb77d3e3a0890c01dd0fdf010a772b20.png)
Le fait qu'il existe deux logarithmes naturels (ln de ln) dans la limite pour la définition constante de Meissel-Mertens peut être perçu comme une conséquence de la combinaison du théorème des nombres premiers et de la limite définissant la constante d'Euler-Mascheroni.
Estimation
La constante de Meissel-Mertens est évaluée à :
- M ≈ 0,26149 72128 47642 78375 54268 38608 69585 9
