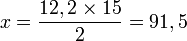Règle de trois - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
La règle de trois, aussi appelée produit croisé, permet de résoudre de nombreux problèmes concernant des phénomènes proportionnels.
Explication
Le principe de la règle de trois consiste à se ramener à l'unité.
Prenons un exemple :
La question que nous souhaitons résoudre est :
- Si pour fabriquer 5 objets il faut 7 heures de travail, combien d'heures faut-il pour fabriquer 8 objets ?
- Déterminons le temps nécessaire à la production d'un objet :
En 7 heures, sont fabriqués 5 objets. Donc la fabrication d'1 objet dure

- Nous pouvons donc en déduire le temps nécessaire à la production de 8 objets :
Si pour 1 objet il faut

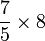
Le terme de Règle de trois provient du fait qu'elle fait intervenir 3 nombres (ici 5, 7, 8). La mise en place d'une règle de trois nécessite une rédaction rigoureuse pour placer ces trois nombres dans la fraction finale. Cette rédaction peut être avantageusement remplacée par un tableau de proportionnalité. De plus, l'utilisation d'un tel tableau permet d'utiliser l'égalité du produit en croix (égalité du produit des diagonales).
Soit x le temps de fabrication de 8 objets : :
| 5 | 1 | 8 |
| 7 |
|
|
Ici, on passe de la première colonne à la seconde colonne en divisant par 5, puis de la seconde colonne à la troisième colonne en multipliant par 8.
- Le nombre manquant est donc x = 11,2h = 11h12min.
Le tableau de proportionnalité permet de raccourcir encore le raisonnement en mécanisant le calcul. On peut trouver directement le résultat de cette façon :
| 5 | 8 |
| 7 |
|
Le résultat final s'obtient en effectuant le produit des deux termes d'une diagonale et en divisant par le terme restant.
-
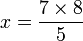
C'est sous cette forme qu'elle est maintenant présentée en France.
Exemples
Exemple 1
Le prix des pommes est de 5 € le kg, j'en achète 1,5 kg, combien devrai-je payer ?
| Kg | Prix en € |
|---|---|
| 1 | 5 |
| 1,5 | x |
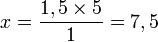
Donc, je devrai payer 7,5 €.
Exemple 2
On dispose d'un plan dont l'échelle indique que : 2 cm
On veut connaître la distance à vol d'oiseau entre 2 villes.
Pour cela, on mesure sur le plan la distance entre les points indiquant le lieu géographique de ces villes. On trouve 12,2 cm.
| Plan | 2 | 12,2 |
| Terrain | 15 | ? |
D'après la règle de trois, on effectue ce petit calcul :
Ainsi la distance sur le terrain est : 91,5 km.