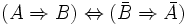Proposition contraposée - Définition

La contraposition (ou modus tollens) est un raisonnement logique basé sur la négation du conséquent d'une implication. C’est-à-dire que puisque la cause d'une implication engendre la conséquence, alors l'absence de la conséquence implique automatiquement l'absence de la cause.

La contraposition est équivalente à une implication dont elle est considérée comme une règle dérivée. Ainsi, la proposition contraposée de la proposition

" A implique B " ("s'il pleut, alors le sol est mouillé")

est

" non-B implique non-A ". ("si le sol n'est pas mouillé, alors il ne pleut pas")

Si la première est vraie, alors la seconde l'est aussi, et inversement.

La contraposition exprime le fait que B est une condition nécessaire de A : on ne peut pas avoir A sans avoir B. Dans notre exemple, il n'est pas possible qu'il pleuve et que le sol ne soit pas mouillé.

Il faut bien distinguer la contraposée de la réciproque : la réciproque de " A implique B " est " B implique A ". Le fait que l'une soit vraie ne dit rien sur l'autre à moins qu'on ait montré, par ailleurs, qu'il existe une équivalence entre A et B (" A si et seulement si B ") auquel cas, l'implication et la réciproque sont toutes deux vraies. Ainsi, même si l'implication "s'il pleut, alors le sol est mouillé" est vraie, on ne peut pas rien dire sa réciproque ("si le sol est mouillé, alors il pleut").

Il ne faut pas confondre non plus la contraposition avec la négation de l'antécédent " non-A implique non-B " ("s'il ne pleut pas, alors le sol n'est pas mouillé") qui, elle, n'est pas équivalente à l'implication. Utiliser la négation de l'antécédent conduit à un raisonnement faux ou sophisme. En effet, dans notre exemple le sol peut avoir été mouillé par autre chose et donc ce n'est pas parce qu'il ne pleut pas que le sol n'est pas mouillé.

Notation

la proposition : " A implique B " se note

A ⇒ B.

nous avons donc :

(A ⇒ B) ⇔ (non-B ⇒ non-A)

que l'on note aussi

ou encore

(A ⇒ B) ⇔ (¬B ⇒ ¬A)

Les lois de De Morgan résument la façon dont il faut permuter en logique les opérations " et " et " ou " lors de transformations de formules. La définition logique de l'implication est la suivante :

(A⇒B) ⇔ ((non A) ou B)

Remarquons que l'implication logique ne présuppose aucune hiérarchie, même chronologique, entre ses éléments constituants, et est donc à bien distinguer de la causalité, en particulier si l'on note en abrégé cette dernière par le même signe " ⇒ ".

Applications

L'équivalence entre implication et contraposition est fréquemment utilisée en logique, au même titre que les identités remarquables en algèbre.

Les deux propositions sont équivalentes logiquement mais elles n'ont pas le même rôle dans une démonstration.

Ainsi, je prends pour exemple le théorème " si un quadrilatère est un rectangle alors il est un parallélogramme ". Il sert à démontrer qu'un rectangle a toutes les propriétés du parallélogramme (côtés opposés parallèles et de même longueur, …).

Sa contraposée, " si un quadrilatère n'est pas un parallélogramme alors il n'est pas un rectangle " sert à démontrer qu'un quadrilatère ne vérifiant pas une des propriété caractéristique du parallélogramme alors il ne peut pas être un rectangle.

Comme on l'a dit plus haut, bien que la contraposée d'un théorème vrai est aussi vraie, sa réciproque peut être fausse : " si un quadrilatère est un parallélogramme alors il est un rectangle " est faux.

Exemple

Enoncé

L'affirmation

Ceux qui parlent ne savent pas

est strictement équivalente à l'affirmation

Ceux qui savent ne parlent pas

Preuve

On substitue simplement A="(parler)" et B="non(savoir)":

    ((parler) ⇒ non(savoir))

⇔ (non(non(savoir)) ⇒ non(parler))

⇔ ((savoir) ⇒ non(parler))

Appellations Différentes

Dans certains établissements d'enseignement, la preuve par contraposée est appelée "preuve par transposition".