Partition (mathématiques) - Définition
Une partition d'un ensemble X est un ensemble P de sous-ensembles non vides de X deux à deux disjoints et qui forment un recouvrement de X. Autrement dit P est une partition de X si et seulement si les parties de P sont non vides et tout élément x de X se trouve dans l'une exactement de ces parties.
Définition
Soit un ensemble X quelconque. Un ensemble P de sous-ensembles de X est une partition de X si :
- Aucun élément de P n'est vide (Dans certaines définitions cette condition est omise) ;
- L'union des éléments de P est égal à X ;
- Les éléments de P sont deux à deux disjoints.
Les éléments de P sont appelés les parties de la partition.
Exemples
L'ensemble {1, 2, 3} a les partitions suivantes :
- { {1}, {2}, {3} },
- { {1, 2}, {3} },
- { {1, 3}, {2} },
- { {1}, {2, 3} } et
- { {1, 2, 3} }.
Remarquons que
- { {}, {1, 3}, {2} } n'est pas une partition parce qu'elle contient l'ensemble vide, noté {} ou
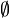
- { {1, 2}, {2, 3} } n'est pas une partition parce que l'élément 2 appartient à plus d'une partie.
- { {1}, {2} } n'est pas une partition de {1, 2, 3} parce qu'aucun de ses éléments ne contient 3 ; c'est une partition de {1, 2}.
Dans le cas où toutes les parties de la partition ont même cardinal, on retrouve le lemme des bergers.
Partitions et relations d'équivalence
Si une relation d'équivalence est donnée sur l'ensemble X, alors l'ensemble de toutes les classes d'équivalence forme une partition de X. Inversement, si une partition P de X est donnée, alors nous pouvons définir une relation d'équivalence sur X notée ~, par x ~ y si et seulement s’il existe une partie de P qui contient à la fois x et y. Les notions de relation d'équivalence et de partition sont donc fondamentalement équivalentes.
Ordre partiel sur les partitions : le treillis des partitions
L'ensemble de toutes les partitions d'un ensemble est partiellement ordonné : par définition, une partition est plus fine qu'une autre si elle fractionne les parties de l'autre en de plus petites parties. Cet ordre partiel forme un treillis complet où la borne inférieure est la partition grossière en un seul sous-ensemble et la borne supérieure la partition en singletons.
Nombre de partitions d'un ensemble fini
- Le nombre de Bell Bn est le nombre de partitions différentes d'un ensemble à n éléments. Les premiers nombres de Bell sont B0=1, B1=1, B2=2, B3=5, B4=15, B5=52, B6=203.
Les partitions par paire
- Le nombre de partitions par paires d'un ensemble à 2n éléments est égal à
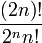
- Une bijection d'un ensemble E sur un ensemble F transforme une partition de E par paire, en une partition de F par paire.
- Tout ensemble infini admet au moins une partition par paire.

















































