Relation bien fondée - Définition

Soit E un ensemble non vide. On dit qu'une relation R sur E est bien fondée ou plus rarement nœthérienne (alors que l'on devrait dire en toute rigueur artinienne ce qui se dit plus rarement encore) si et seulement si elle vérifie l'une des deux conditions suivantes, équivalentes d'après l'axiome du choix dépendant (une version très faible de l'axiome du choix) :

• Pour toute partie X de E, il existe un élément x de X n'ayant aucun R-antécédent dans X
  (un R-antécédent de x dans X est un élément y de X vérifiant yRx) ;
• Il n'existe pas de suite infinie (x_n) d'éléments de E telle qu'on ait x_n+1Rx_n pour tout n.

Exemples

• Sur l'ensemble des arbres binaires finis, construits à partir de l'arbre vide et de l'enracinement ¤ (c'est-à-dire qu'à partir de deux arbres A et B on forme l'arbre A ¤ B), l'ordre strict " est un sous-arbre strict de " est un ordre bien fondé. Il se signifie ainsi: A ¤ B > ou A ¤ B > C si A C ou B C.
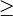
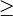
• Sur l'ensemble des chaînes de caractères, l'ordre strict " est préfixe strict de " et bien fondé.
• Sur l'ensemble des chaînes de caractères, l'ordre du dictionnaire n'est pas bien fondé.
• L'ordre strict associé à un bon ordre.
• De manière générale une relation d'ordre total est un bon ordre si et seulement si la relation stricte associée est bien fondée.
• L'axiome de fondation exprime que la relation d'appartenance est bien fondée.
• Sur l'ensemble des arbres binaires, on peut définir l'ordre bien fondé > suivant :
  • A ¤ B > ,
  • ou A ¤ B > C ¤ D parce que
    • A > C et A ¤ B > D,
    • ou A = C et B > D

On notera que dans le dernier ordre, l'arbre ( ¤ ) ¤ a une infinité d'arbres plus petit que lui.

Usage en algorithmique

Sans entrer dans les détails, une conséquence directe et quasi-triviale de la définition d'un ordre strict bien fondé est qu'un algorithme, qui construit une suite d'éléments d'un tel ordre tout en assurant qu'un élément construit est strictement inférieur à son prédécesseur, assure aussi sa terminaison (prouvé par l'absurde : en effet, dans le cas contraire on construirait une suite infinie strictement décroissante).

Les structures utilisées en algorithmique (types construits) étant souvent des ordres stricts bien fondés, on dispose ainsi d'une méthode très générale pour prouver la terminaison d'un programme informatique.

Relation bien fondée et récurrence

À une relation bien fondée est associée une fonction de rang construite par récurrence transfinie, ce qui permet des démonstrations par récurrence transfinie. Voyons cela de plus près.

Soient R une relation bien fondée sur un ensemble E et J un ensemble bien ordonné, de cardinal supérieur à celui de E, nous servant de " réservoir d'ordinaux " (ses premiers éléments sont 0,1,...). La fonction de rang ρ de R est l'application de E dans J définie par récurrence transfinie comme suit : pour x∈E

• ρ(x) = 0 si x n'a pas d'antécédent pour R ;
• ρ(x) = sup { ρ(y)+1, y antécédent de x pour R } dans le cas général.

Ainsi le rang de x est le plus petit ordinal strictement supérieur aux rangs des antécédents de x ; il peut être de première ou deuxième espèce. La longueur de la relation R, souvent notée |R|, est le plus petit ordinal strictement plus grand que tous les ρ(x). La fonction de rang permet d'organiser E en une hiérarchie de manière évidente, très utilisée en théorie axiomatique des ensembles avec pour R la relation d'appartenance.

La fonction de rang permet de faire des démonstrations par récurrence transfinie à l'aide du théorème suivant qui généralise l'axiome de Peano n°5 ou le principe de récurrence :

Soit P une partie de E contenant, pour tout j, tous les x∈E de rang j dès qu'il contient tous les x de rang < j. Alors P est l'ensemble E tout entier.

Grâce à l'ensemble vide, ensemble des x de rang <0, on n'a pas eu besoin de démarrer la récurrence explicitement. Attention ! Il ne suffit pas ici de passer du rang j au rang j+1 à cause de l'existence d'ordinaux de deuxième espèce.