Théorie axiomatique des ensembles - Définition

Il existe plusieurs versions formelles de la théorie des ensembles, mais quand on parle de " la " théorie axiomatique des ensembles, on désigne habituellement sous ce nom la théorie ZFC. Au XXI^e siècle, c'est la théorie sur laquelle la majorité des mathématiciens s'appuient, mais il existe d'autres théories concurrentes.

Certaines sont simplement des variantes, d'autres reposent sur des approches différentes. Citons à titre d'exemple la théorie des types (abandonnée à cause de sa lourdeur), la théorie NBG (de von Neumann, Bernays et Gödel) qui introduit la notion de classe, ou les théories de Quine…

Les origines d'une théorie rigoureuse des ensembles

Cantor est le principal créateur de la théorie des ensembles, sous une forme que l'on qualifie aujourd'hui de théorie naïve des ensembles. Mais, à côté de considérations élémentaires, sa théorie comportait des niveaux d'abstraction élevés. La vraie nouveauté de la théorie de Cantor, c'est qu'elle permet de parler de l'infini. Par exemple, une idée importante de Cantor a été de définir l'équipotence. Deux ensembles A et B sont équipotents, ou ont même cardinalité (même nombre d'éléments quand ils sont finis), s'il existe un moyen d'associer à chaque élément de A un et un seul élément de B et inversement. On peut ainsi démontrer que l'ensemble des entiers naturels a la même cardinalité que l'ensemble des nombres rationnels, bien que soit un sous-ensemble propre de . Ces deux ensembles sont dits infinis dénombrables. D'un autre côté, l'ensemble des nombres réels n'a pas la même cardinalité que ou , mais une cardinalité supérieure : il est dit indénombrable ou non dénombrable. Cantor a donné deux preuves que n'est pas dénombrable, et la deuxième, qui utilise un argument connu sous le nom d'argument de la diagonale de Cantor, a été extraordinairement influente et a eu de nombreuses et diverses applications en logique et en mathématiques.

Cantor a approfondi la théorie et a construit des hiérarchies infinies d'ensembles infinis, les nombres ordinaux et les nombres cardinaux. Ces constructions étaient controversées à son époque, l'opposition étant conduite par le finitiste Léopold Kronecker ; mais aujourd'hui elles sont acceptées par la majorité des mathématiciens.

Le développement de la théorie des ensembles par Cantor était encore " naïf " dans le sens qu'il n'employait pas encore une axiomatique précise, et parce que pour lui il n'y avait qu'une seule théorie des ensembles, un seul univers ensembliste attendu, alors que les théoriciens des ensembles d'aujourd'hui jonglent avec des univers différents.

Après coup, on a pu simplifier, assez injustement pour Cantor, en résumant sa théorie à un usage tacite de l'axiome d'extensionnalité, et d'une version trop forte du schéma d'axiomes de compréhension, qui en substance permettrait d'associer à toute propriété l'ensemble des objets vérifiant cette propriété. Une telle théorie, que l'on n'attribuera pas à Cantor, est contradictoire. Elle mène à deux famille de paradoxes. Les uns, comme le paradoxe de Berry ou le paradoxe de Richard, se rattachent au fait que le langage n'est pas bien défini, les autres, comme le paradoxe de Russell à un usage trop large de la compréhension : quand on essaie de construire l'ensemble S = {A | A n'appartient pas à A} de tous les ensembles qui n'appartiennent pas à eux-mêmes on tombe sur une contradiction. L'actuel schéma d'axiomes de compréhension, proposé par Zermelo, est restreint afin d'éviter ce paradoxe.

Cantor connaissait, avant la découverte du paradoxe de Russell, des paradoxes plus complexes, mais de même nature, comme le paradoxe de Burali-Forti ou le paradoxe du plus grand cardinal. Beaucoup de théoriciens des ensembles s'entendent pour dire que l'axiomatisation la plus adéquate à la théorie développée par Cantor est la théorie ZFC avec axiome de fondation (voir ci-dessous), ou la théorie des classes de von Neumann, Gödel et Bernays, qui lui est, en un certain sens (qui peut être rendu précis), équivalente.

Au tournant du siècle, Cantor est de plus en plus handicapé par sa maladie nerveuse, mais ses solutions aux paradoxes circulent par sa correspondance et sont connues, à la fin du XIXème siècle, de Richard Dedekind et, à Göttingen, de David Hilbert et de Ernst Zermelo. Cependant, pour beaucoup de mathématiciens de l'époque, les paradoxes jettent un doute sur la validité de la théorie des ensembles, les solutions proposées par Cantor sont trop informelles pour convaincre ceux qui les connaissent. Certains s'orientent vers la méthode axiomatique, illustrée à la même époque par Hilbert pour les fondements de la géométrie (1899).

Ainsi, en 1908, Ernst Zermelo construit un système d'axiomes pour la théorie des ensembles. En dehors de l'axiome d'extensionnalité, on peut voir ces axiomes comme une restriction de la version contradictoire du schéma d'axiomes de compréhension aux cas particuliers utiles, qui ne permettent pas de dériver les paradoxes. Dans ce système, il inclut également l'axiome du choix (qui n'a rien à voir avec la compréhension), un axiome à l'époque très controversé, avec lequel il a montré (en 1904) le théorème du bon ordre, et qui a également été utilisé implicitement par Cantor. Ce système a été redéfini de façon plus formelle et complété dans les années 1920 par Abraham Adolf Fraenkel et Thoralf Skolem, qui ajouteront le schéma d'axiomes de remplacement (autre cas particulier de la compréhension non restreinte), donnant la théorie ZFC connue aujourd'hui.

Le problème de l'axiome du choix

Il y a plusieurs raisons pour lesquelles l'axiome du choix a été controversé et l'est encore aujourd'hui, aussi bien par certains des mathématiciens travaillant en mathématiques pures, que par de nombreux autres travaillant en mathématiques appliquées.

Une de ces raisons est que l'axiome du choix paraît intuitivement vrai pour les mathématiciens platoniciens, cela leur parait tellement évident qu'il leur semble étrange de devoir l'inclure dans les hypothèses nécessaires pour pouvoir démontrer certains théorèmes qui leur paraissent à eux aussi (les platoniciens) intuitivement vrais. La situation est compliquée par le fait qu'il est indépendant des autres axiomes de la théorie ZF (c'est-à-dire ZFC sans l'axiome du choix). On peut donc créer deux sortes de mathématiques distinctes et toutes deux parfaitement valides, l'une acceptant l'axiome du choix et l'autre le niant. Le refus d'incorporer cet axiome ou sa négation mène à l'élimination d'un énorme pan des mathématiques (par exemple, la plus grande partie de ce qui a trait aux nombres réels) et son remplacement par une théorie qu'il resterait à élaborer.

Une autre raison est que, bien que l'axiome du choix permette de construire certaines parties des mathématiques, son utilisation conduit à certains résultats sans relation ou parfois contraires aux conceptions usuelles, et implique l'existence d'objets bizarres, contre-intuitifs. Un des meilleurs exemples de ces étrangetés est certainement la paradoxe de Banach-Tarski qui, en utilisant l'axiome du choix, affirme qu'on peut découper une sphère en un nombre fini de morceaux, les déplacer par une suite de mouvement rigides (translation et rotation), en permettant à certaines pièces d'en traverser d'autres et de les rassembler en formant deux copies de la sphère d'origine. Il serait donc possible de violer par exemple la loi de conservation des masses en physique. Cependant, après analyse, il n'y a pas de paradoxe, simplement une complication : le théorème souligne seulement que notre notion intuitive de volume n'existe pas en mathématiques.

Finalement, l'emploi de cet axiome ne permet pas de faire des démonstrations constructives, c'est-à-dire qui fournissent une méthode permettant d'effectuer les calculs ou de trouver une solution, mais permet seulement de montrer qu'une telle solution existe; ce que réprouvent les partisans de l'intuitionnisme.

Il est à noter qu'il existe aujourd'hui d'autres solutions que simplement accepter ou nier l'axiome du choix ; il est ainsi possible de le remplacer par une variante plus faible, tel l'axiome du choix dépendant.

Les axiomes de la théorie ZFC

La théorie qui se base sur les axiomes originaux de Zermelo est appelée théorie de Zemerlo ou théorie Z. Si on la complète par l'axiome de remplacement de Fraenkel, on obtient la théorie de Zermelo-Fraenkel, ou plus simplement la théorie ZF, bien que la forme finale des axiomes soit due à Skolem. Lorsqu'on lui adjoint l'axiome du choix, un axiome qui était plus controversé au moment de l'élaboration de ces théories qu'il ne l'est aujourd'hui, on obtient alors la théorie dite ZFC (" C " pour " choix ").

Un aspect important de la théorie ZFC est que tous les objets dont elle traite sont des ensembles et ne peuvent être que des ensembles. En particulier, chaque élément d'un ensemble est lui-même un ensemble. D'autres objets mathématiques familiers, tels que les nombres, doivent donc par conséquent être définis en termes d'ensembles.

Strictement parlant, les axiomes de ZFC sont simplement des énoncés du calcul des prédicats du premier ordre égalitaire dans un langage ayant un seul symbole primitif pour l'appartenance (relation binaire). Ce qui suit doit donc seulement être perçu comme une tentative d'exprimer en français la signification attendue de ces axiomes. De plus, l'axiome de séparation (ou compréhension) et l'axiome de remplacement sont en fait des schémas infinis d'axiomes.

1. Axiome d'extensionnalité : Si deux ensembles ont les mêmes éléments, alors ils sont identiques.
2. Axiome de l'ensemble vide : Il existe un ensemble sans élément. On le note (ou plus rarement {}). Cet axiome ne fait pas à proprement partie de l'axiomatisation de ZFC : c'est une propriété générique des modèles du calcul des prédicats de posséder au moins un élément. On en déduit par le schéma d'axiomes de compréhension l'existence de l'ensemble vide.
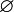
3. Axiome de la paire : Si x et y sont deux ensembles, alors, il existe un ensemble contenant x et y et eux seuls comme éléments. Cet ensemble se note {x,y}. Notez que x et y ne sont pas nécessairement distincts.
4. Axiome de la réunion : Pour tout ensemble X, il existe un ensemble R dont les éléments sont précisément les éléments des éléments de X et eux seuls.
5. Axiome de l'ensemble des parties : Pour tout ensemble E, il existe un ensemble dont les éléments sont précisément les sous-ensembles de E. Cet ensemble se note habituellement P(E).
6. Axiome de l'infini : Il existe un ensemble W dont est élément et tel que pour tout x appartenant à W, appartient aussi à W. On peut ensuite définir par compréhension l'intersection de tous les ensembles contenant et clos par cette opération : il s'agit de l'ensemble des entiers de von Neumann.
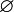
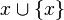
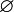
7. Schéma d'axiomes de compréhension ou de séparation : pour tout ensemble A et toute propriété P exprimée dans le langage, il existe un ensemble dont sont éléments les éléments de A vérifiant P. Le schéma de compréhension est conséquence du schéma de remplacement qui suit.
8. Schéma d'axiomes de remplacement : Pour tout ensemble A et toute relation binaire P, formellement définie comme une proposition P(x,y) et telle que P(x,y) et P(x,z) impliquent que y = z, il existe un ensemble contenant précisément les images par P des éléments de l'ensemble d'origine A.
9. Axiome de fondation : Tout ensemble X non vide contient un élément y tel que X et y sont des ensembles disjoints (qui n'ont aucun élément en commun), ce qui se note . Cet axiome n'est pas toujours ajouté à Z ou ZF. On peut construire assez facilement comme sous-classe d'un modèle quelconque de ZF, un modèle de ZF vérifiant l'axiome de fondation. Les ensembles utiles au développement des mathématiques appartiennent à cette sous-classe.
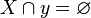
   Ajouter ou ne pas ajouter l'axiome de fondation n'a pas grande incidence pour le développement des mathématiques usuelles en théorie des ensembles.
10. Axiome du choix : (version de Zermelo) Étant donné un ensemble X d'ensembles non vides mutuellement disjoints, il existe un ensemble y (l'ensemble de choix pour X) contenant exactement un élément pour chaque membre de X.
    L'axiome du choix reste controversé pour une minorité de mathématiciens. Des formes faibles existent, comme l'axiome du choix dépendant, indispensable pour le développement de l'analyse réelle.

L'indépendance dans la théorie des ensembles

De nombreux énoncés sont indépendants de la théorie ZFC. Cette indépendance est généralement prouvée par la méthode dite du forcing, c'est-à-dire en montrant que chaque modèle transitivement dénombrable de la ZFC (plus parfois des axiomes de grands cardinaux) peut être étendu pour satisfaire l'affirmation en question ainsi que, par une voie différente, sa négation. Une preuve d'indépendance par forcing prouve automatiquement l'indépendance vis-à-vis des affirmations arithmétiques, des autres affirmations concrètes et des axiomes de grands cardinaux.

Voici quelques affirmations dont l'indépendance est démontrable par forcing:

• l'hypothèse du continu ;
• le principe du losange ;
• l'hypothèse de Suslin ;
• l'hypothèse de Kurepa.

Note: Le principe du losange implique l'hypothèse du continu et la négation de l'hypothèse de Suslin. L'univers constructible satisfait l'hypothèse du continu généralisée, le principe du losange et l'hypothèse de Kurepa.